こんにちは。データ分析チームの米谷悠です。

フューチャーアーキテクトのデータ分析チームは各プロジェクトと連携しながら、いま流行りのDeepLearning等を使った画像処理・自然言語処理や、従来からある多変量解析や機械学習の方法を使った社会科学・経済・マーケティング・経営組織等に関するデータの分析を行っています。こうしたデータサイエンス領域における基礎の1つとして統計学があることはみなさんもご存知かと思います。本Blogでは日常のニュースで報道される数字を統計学的に説明することによって、統計学の基本的な考え方に触れていきたいと思います。 ¹。

内閣支持率を統計学を使ってより厳密に説明

みなさんも「世論調査」や「内閣支持率」という言葉をニュース等で耳にすると思います。よく知られている世論調査は新聞各社等を中心に行われ、内閣支持率はその調査項目の1つです。

つい先日も日本経済新聞とテレビ東京が世論調査を行い、2017年2月27日（月）の同新聞朝刊の記事には

内閣支持率は1月の前回調査と比べて～（中略）～60%だが、引き続き高い水準を保つ。

とありました。さらに

調査は日経リサーチが24～26日に全国の18歳以上の男女に携帯電話も含めて乱数番号（RDD方式）による電話で実施。1001件の回答を得た。回答率は47.4%。

とありました。

今回は、統計学の基礎知識を使って、この内閣支持率のより厳密な説明を試みます。具体的に、この世論調査の結果はある条件のもとで「全国の有権者全員に調査したらわかるはずの内閣支持率が60％であると推定された。また、当該内閣支持率が、推定された60％の前後3％ポイント（57％～63％）の間に存在する確率が95％で、存在しない確率は5％である」 と言うことも可能となります。

「内閣支持率は60％ではないの？」と思われた方もおられるかもしれません。上記のように言える理由を以下でご説明します。

「世論調査で本当に知りたかったこと」と統計調査

そもそも世論調査で本当に知りたかったことは何でしょうか？ それは新聞記事では明示されていませんが、「もし全国の有権者全員に調査できたとすると、わかるはずの内閣支持率」です ²。これは国政等においてとても重要な値です。

では、なぜ全国の有権者全員に調査しないのでしょうか？ それはコストの問題から非現実的であることは明らかです。これに対して、全国の有権者の一部であれば今回の世論調査のように調査することが可能です。

統計学では、全国の有権者全員を 母集団、実際に電話が掛かってきた有権者を 標本 と言います。そして、本Blogでは「もし全国の有権者全員に調査できたらわかるはずの内閣支持率」を 母支持率、実際に電話が掛ってきた有権者への調査でわかった内閣支持率60％を 標本支持率 と呼ぶことにします。

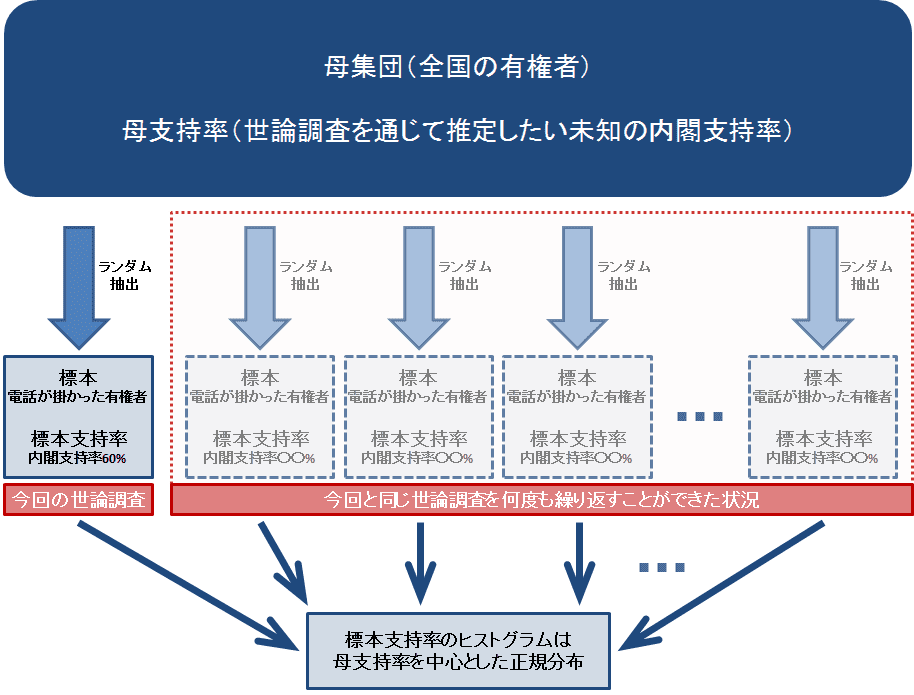
次に、標本は今回の世論調査と同じように選ばれる必要があります。つまり、まず標本は母集団から選ばれなければいけません。有権者でない方に調査を行うよりも、有権者に調査を行った方が、より適切な結果が得られることはおわかりいただけると思います。

また、標本は母集団からランダムに（今回の世論調査では乱数番号（RDD方式）を使って）選ばれる必要があります。仮に、全国の有権者全体において内閣を支持する有権者と支持しない有権者が半々（つまり母支持率50％）だったとして、意図的に内閣を支持する有権者だけを標本として調査を行うと、標本支持率は100％となり、調査対象と結果に偏りがあることから、母集団の状況をより正確に表すことができていません。

「同じ調査を何度も繰り返すことができた状況」を想定することが基本的なアイデア

以上のようにして得られた標本支持率60％は、本当に知りたかった母支持率と一致しているのでしょうか？ 必ずしも一致するとは限りません。例えば、母支持率が60％のときに、ランダムに1,001人の標本を抽出したところ、偶然にも全員が内閣支持者（標本支持率100％）となることは、 という僅かな確率ですが起こりえます。

では、標本支持率と母支持率の関係はどうなっているのでしょうか？ 実は、母集団から標本をランダムに選んでいたことで、標本支持率60％はある性質を持ちます。以下ではこのことをご説明して、世論調査の内閣支持率を統計学を使ってより厳密にお伝えすることを試みます。

まず、今回と同じ世論調査を、同じ条件で何度も繰り返すことができたとしましょう。つまり、同じ時点で同じ母集団からランダムに標本を選んで標本支持率を計算するというプロセスを何度も繰り返すことができたとします。標本は毎回ランダムに選ばれているので、標本も標本支持率も毎回異なるはずです。

そして、各回で得られる標本支持率を集めて、そのヒストグラム(ある集団の個々の数値の分布を視覚化するグラフ)を書くことができたとしたら、それは母支持率を中心とする正規分布に近似できることが統計学の理論上知られています（中心極限定理）。つまり、調査回数分だけある標本支持率は、その多くが母支持率の近傍にある一方、母支持率から遠く離れた値も僅かな確率で取りうるということです。

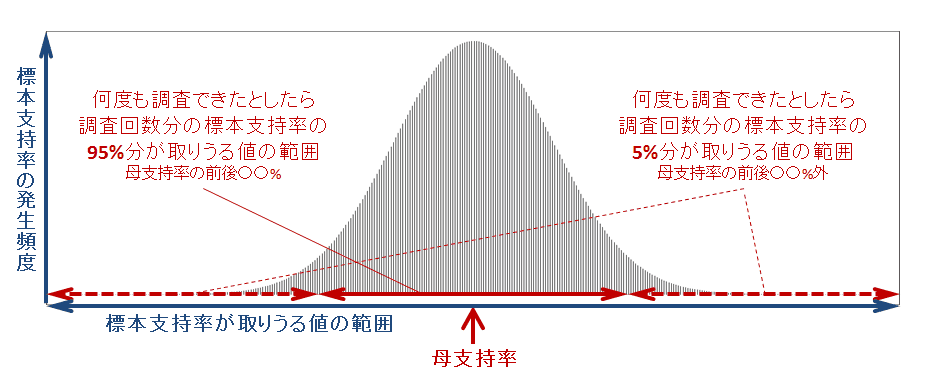
そして、実際に行われた今回の1回の世論調査で得られた標本支持率60％は、近似した正規分布の相対頻度にしたがって、母支持率の周辺のどこか1つの値を取っていると考えられるようになります。

「世論調査で本当に知りたかった内閣支持率」と「調査結果の内閣支持率60％」の関係

では、実際に行われた今回の1回の世論調査で得られた1つの標本支持率と母支持率の具体的な関係はどうなっているのでしょうか？

まず、近似できる正規分布の散らばり具合を表す標準偏差を、今回の1回の世論調査の標本データ（標本支持率は「支持する」を1、「支持しない」を0）から推定できます。そして、その標準偏差の推定値と正規分布の理論式を組合せることで、何度も同じ調査を繰り返すことができたら得られる調査回数分の標本支持率の95％分が、母支持率の前後〇〇％の間で発生しうるということを（例えば100万回調査を行ったら95万回分の標本支持率が発生しうる区間を）具体的に推定できます。このことは、反対に5％分（5万回分の標本支持率）が母支持率の前後〇〇％より外の値と推定できることも意味します ³。

このことから、今回の1回の世論調査で得られた標本支持率60％は、95％の確率で母支持率の前後〇〇％の間にあると推定されると言えることになり、それは反対に標本支持率60％の前後〇〇％の間に母支持率がある確率が95％と推定されると言えることにもなります。

同様に標本支持率60％の前後〇〇％の間に母支持率がない確率が5％と推定されるとも言えます。つまり、世論調査の内閣支持率60％が、もし全国の有権者全員に調査したらわかるはずの本当に知りたい母支持率から大きく外れている可能性も僅かながらありうるということです。

より厳密な説明例

もし仮に今回の世論調査が、前述の条件に加えて次の2つの条件のもとでも行われているとすれば、母支持率の周辺の95％分の標本支持率が発生する区間は、母支持率の前後3％ ⁴と推定されます。

1. 全国の有権者全員を何らかの属性で分けた上で、各属性内でランダムに標本を選んでいるのではなく、全国の有権者全員を1つの層としている。
2. 回答率が47.7％ではなく100％である、もしくは回答と非回答がランダムに発生している ⁵。

以上の条件のもとでは、冒頭に書いたように「国の有権者全員に調査したらわかるはずの内閣支持率が60％であると推定された。また、当該内閣支持率が、推定された60％の前後3％（57％～63％）の間に存在する確率が95％で、存在しない確率は5％である」と言うことができます。

最後に

今回は世論調査で調べられている内閣支持率を、統計学の基本的な知識を用いて、より厳密にお伝えすることを試みました。いかがだったでしょうか？

公表されている内閣支持率が、全国の有権者全員に調査したらわかるはずの内閣支持率とは必ずしも一致せず、僅かな確率ではありますが、大外れしている可能性もあるということは、聞いてみれば当たり前かもしれませんが、少し驚かれた方もおられるのではないでしょうか？

フューチャーアーキテクトは、ITの分野において原理原則を重視するマインドが非常に強いですが、それはデータ分析においても同じです。

データ分析、機械学習、AIといったデータサイエンス領域において基礎的要素の1つである統計学も疎かにせず業務の方を推進しておりますので、今後ともよろしくお願いします！！