はじめに
こんにちは。TIG DXチームの村瀬です。
公開鍵暗号
公開鍵で暗号化されたデータは対応する秘密鍵でしか復号できない。 |
最初にこの説明を聞いた時にそんな鍵がありえるのか? と疑問に思いました。
技術力もなかった当時は不思議で仕方ありませんでした。自分で利用することもないし、知識として覚えておこうぐらいの感覚でいたのですがある程度技術力がついた今日では、常日頃からHTTPSやSSHで利用していることにふと気が付き自分の理解のため仕組みについて公開鍵暗号の1つであるRSA暗号について調べてみることにしました。
RSA暗号を解説しているページはたくさんありますが、この記事では極力簡単な内容になることを心がけてみました。
暗号化、復号の概要
図で表すとこんな感じです。
暗号化式と復号式
RSA暗号ではべき乗と余り(mod)を利用します。
暗号化する際はとある数EとNを利用します。
復号する際も式は同様ですがEの代わりにDを利用します。
式から暗号文を削除すると以下の式が成り立ちます。
とりあえずだまされたと思って確認
平文を5,とある数E,D,Nを3,7,33として確認してみます。
暗号化
復号
平文の5が暗号化することで26になり、26を復号することで5に戻りましたね。modが33なので平文が1~32の整数であれば同様に暗号化、復号すれば元の平文に戻すことができます。
E,D,Nの求め方
暗号化、複合に用いたE,D,Nはどんな数字でも良いわけではありません。
では、暗号化、復号が成り立つE,D,Nはどのような数なのでしょうか?
任意の正の整数a,nと、相違なる素数p、qにおいて以下の式が成り立ちます。
どうして成り立つのかは省略しますがRSA暗号の発明者が発見したぐらいに思ってください。
RSA暗号の肝はこの数式です。NからE,Dを探せばRSAで暗号化、復号ができます。
先の例ではNが33でしたのでそれを素因数分解してp,qは3,11です。ここからE,Dを求めます。
ここまで触れていませんでしたがE,Dは素数である必要があります。素数同士のかけ算で21になるE,Dの組み合わせは3,7※ですね。
※説明のためにしれっと素因数分解していますが、実際の鍵生成ではEを固定値にすることで容易にDを求めています。
秘密鍵が容易に特定されるのでは?
今回の場合、暗号する為には秘密鍵として3,33の数字の組が必要で、複合する為に公開鍵として7,33の数字の組が必要です。上記のE,D,Nの求め方の計算方法を用いれば公開鍵がわかれば秘密鍵も簡単にわかってしまいそうです。では、実際に私たちが利用している秘密鍵はなぜ特定が困難なのでしょうか?
それは素因数分解が容易にできないことを利用し特定を困難にしています。
二桁程度の素因数分解は人間でも瞬時に計算できますが、数百桁の素因数分解はコンピュータを利用しても容易には計算できません。
ですので実際に利用されている鍵はとても大きな数を利用しています。
数字が暗号化出来るのはわかったけど文字列を暗号化したいんだけど?
コンピュータで取り扱われる文字は文字コードで成り立っています。文字コードは1つ1つの文字が数値から成り立っているので数値として扱われます。
それを一文字ずつ暗号化しているので文字列でも暗号化できます。
例えばFutureをASCII文字コードにすると70,117,116,117,114,101になります。
暗号化と復号に利用する鍵
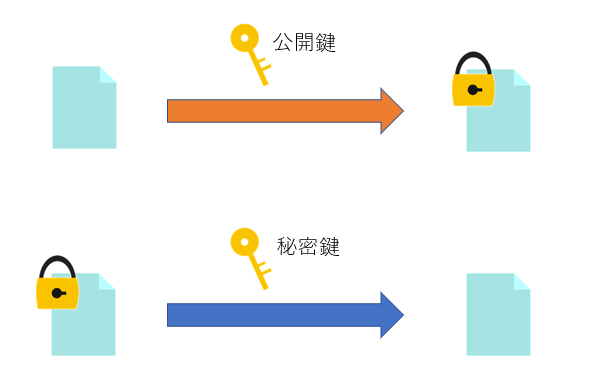
公開鍵を利用して暗号化、秘密鍵を利用して復号できるってことは逆に秘密鍵を利用して暗号化、公開鍵を利用して復号もできるのでは?
はい。鍵を逆に利用してもできます。
重要なのは暗号化した鍵で復号できず、対となる鍵でしか復号できないことです。詳細は割愛しますがこれは実際に電子署名で利用されています。
さいごに
エンジニアでなくともインターネットを利用する人であればHTTPSの裏などで身近に公開鍵暗号が意識することなく利用されてます。
暗号化の原理を知らずに利用していましたが調べてみると面白く、素晴らしさを実感できました。
暗号化、復号に利用される計算式は中学生までに習う足し算、引き算、かけ算(べき乗)、余り(mod)、素数だけで成り立っていることに驚きました。RSA暗号の発明は難産だったようですが発明者って本当に頭が良いですね。
なお、この記事を作成する上で以下のページを参考にさせていただきました。