アルゴリズムとデータ構造連載の3日目です。

除算・平方根の計算のためのハードウェアアルゴリズム

CPUには除算や平方根といった比較的複雑な計算が必要な演算を行うハードウェアが実装されています。除算は、筆算に対応するような単純な方法で計算すると、ビット数nとしてO(n)の計算ステップ（≒CPUサイクル数）がかかります。

しかしながら、50年以上前から、これらをより高速に計算するアルゴリズムが開発され、ハードウェア上で実装されています。

教科書にも載るくらい代表的なものとしてニュートン・ラフソン法（以下、ニュートン法）を利用するものがあります。本ページではこれを解説してみます。

ニュートン法による除算計算アルゴリズム

ニュートン法により除算の計算結果の近似値を反復的に求め続けることで、計算結果に必要なだけの精度で除算結果が得られます。

ニュートン法とは

ニュートン法は数値計算のアルゴリズムの一種で、実数値関数 f に関してとなるを求めるものです。

https://ja.wikipedia.org/wiki/ニュートン法

初期値をとし、近似値をとして、以下の漸化式で次の近似値を求めます。

グラフで幾何的に考えると、ととの交点から接線を引いて、その接線がx軸に交わる点を次の近似値とする、という意味合いになります。

図で表現すると以下です。

※ http://www.akita-pu.ac.jp/system/elect/ins/kusakari/japanese/teaching/Old/Programming/2005/note/6/Slide02.html より引用

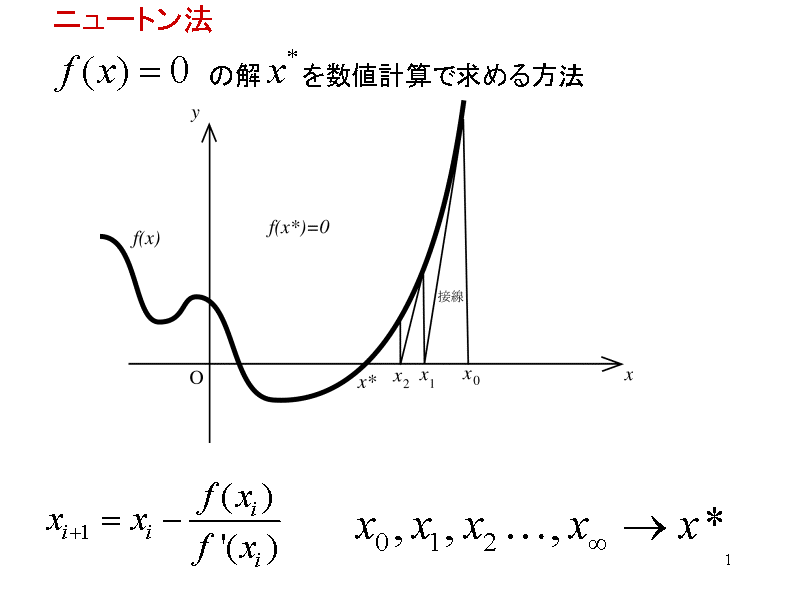
計算結果の誤差

一般的に、ニュートン法による近似値と真値との誤差は、前計算ステップの誤差の二分の一になること（二次収束すること）を示すことができます。

すなわち、誤差は計算ステップに対して指数的に減少(!)し、数値の二進展開における正しい桁数の長さが、計算ステップごとに倍になっていきます。

よくあるの例を計算してみました。

$真値計算値初期値$

除算への適用

除数に対してとおいて、ニュートン法によりの逆数を数値的に求めます。

このとき漸化式は

となります。

ビット数として最下位ビットまで正確に計算するのに必要な計算ステップ数はとなります。

平方根への計算

開平対象の値をに対してとおいて、ニュートン法によりを数値的に求めます。

このとき漸化式は

となります。

参考：開平を計算するコード（Ruby)

実装例として入力にを与えると、ニュートン法によりをRubyで計算します。

require 'bigdecimal'
N,_=gets.chomp.split(' ').map{|n| n.to_i}

x = BigDecimal(N)
# sqrt N
puts x
for i in 0..5
	x = x - (x**2 - N) / (2 * x)
	puts x
end

まとめ

CPUの演算器の実装としてハードウェアアルゴリズムがはるか昔から研究されている
ニュートン法による除算や開平のアルゴリズムが有名
ニュートン法は二次収束するため計算ステップに対して指数的に誤差が減少する