Future Tech Blog
フューチャー技術ブログ
Programmingカテゴリ

monotone minima による高速化について

はじめに

2021年4月入社の山田です、アルゴリズムとデータ構造連載の7日目です。

私は学生時代競技プログラミングに打ち込んでおりました。今回フューチャー技術ブログでアルゴリズムの記事を書く機会を頂きとても嬉しいです！ よろしくお願いします！

内容

本記事では、最適化問題を解く上でのシンプルな高速化手法である monotone minima について説明します。
対象とする問題について紹介した後、 monotone minima のアルゴリズムの説明、そしてなぜ高速化が達成されるのかを説明します。

例題と問題の定式化

まず、イメージしやすいよう以下のような例題を考えてみます。

A市では大通り (ここでは 軸とします) に沿って 軒の家が並んでいます｡ A市には 個のコンビニエンスストアが存在し､ 軒の各家の住人はそれぞれ家に最も近いコンビニエンスストアを普段利用しています｡ A市は家ごとにどのコンビニを普段利用しているかを調査することにしました｡

家の座標 とコンビニの座標 が与えられるので､各家 についてどのコンビニを利用しているかを求めてください｡
(簡単のため座標は、 および が成り立つように並べられているものとします。)

簡単に図で例を示します。A市は2次元平面で表され、赤い丸が家、青い丸がコンビニを表しています。

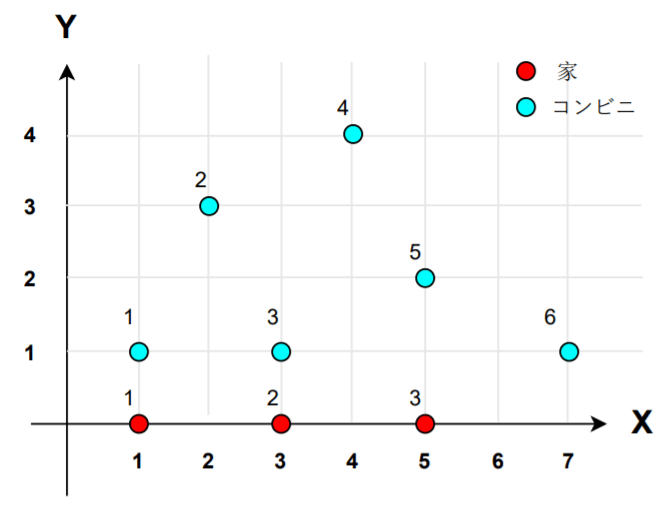
問題イメージ

それぞれの赤い丸 に対して、 最も距離が近い場所にある青い丸 を見つけるということが今回の問題で求められていることです。
ここで、この問題はより一般的にこのように言い換えることができます。

関数 について､各 ごとに最小の値を実現する の値を求めてください｡
( は整数 )

例題では は 家 と コンビニ の距離です。
この問題は特に何も制約がない場合、 のペアを全て試す 時間のアルゴリズムによって解くことができます。
しかし、今回の例題のような場合には の持つ良い性質によって、より高速に問題を解くことが可能です。

monotone minima

では例題の関数 の持つ性質とはどのようなものでしょうか。
それは以下の性質です。

であるような任意の に対して､
の最小を与える を 、 の最小を与える を とした時に、 を満たす。

以降、これを性質 とします。
実際に先程図示した例で見てみましょう。 家とコンビニの距離 を表にするとこのようになります。
赤い文字で示されているところが最小値です。
(注：わかりやすいように実際には距離(ユークリッド距離)の2乗を示しています。)

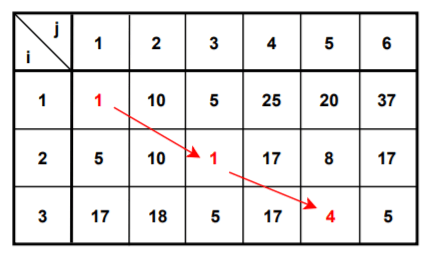
家とコンビニの距離

が大きくなるにつれて、 最小を達成する の値も大きくなっていることがわかると思います。
これはどのような入力に対しても成り立ちます。

が性質 を持つとき、 monotone minima と言われるアルゴリズムが適用でき、 時間で問題を解くことができます。
monotone minima は を適切な順番で計算していくことによって、計算の必要な の範囲を絞っていき、効率的に計算を行うアルゴリズムです。
monotone minima のアルゴリズムを擬似コードで以下に示します。

// i0 <= i <= i1 を満たす i について答えを求めていく関数
// この時､ j0 <= j <= j1 を満たす j について考えれば十分ということが分かっている
def monotone_minima(i0, i1, j0, j1):
    // 対応する i の範囲が存在しない
    if(i0 > i1) return

    // i0 と i1 の真ん中に存在する im に注目する
    im = (i1 - i0) / 2 + i0
    // f(im, j) が最小となるような j (j0 <= j <= j1) を全探索する
    jm = calc_argmin_f(im, j0, j1) // f(im, jm) が最小だとわかった
    answer[im] = jm // 答えを格納

    // 探索の領域を im を中心に半分に分割する
    // i0 <= i < im の範囲の答えを再帰的に求める
    // この時､性質(A)から答えは j0 <= j <= jm の中に存在する
    monotone_minima(i0, im - 1, j0, jm)

    // im < i <= i1 の範囲の答えを再帰的に求める
    // この時､性質(A)から答えは jm <= j <= j1 の中に存在する
    monotone_minima(im + 1, i1, jm, j1)

// 問題全体としては､全ての i (1 <= i <= N) ついて答えを求めたい
// はじめは 1 <= j <= M を満たす全ての j について考えなければ行けない
def solve_all():
    monotone_minima(1, N, 1, M)

solve_all()によって全ての についての答えを計算できます。
性質 からこのアルゴリズムが正しい答えを計算することがわかります。

高速化が達成される理由

では、これでなぜ高速化が達成されるのでしょうか？ 問題の分割されていく流れに注目して計算にかかる時間を考えてみます。
の値が書かれた表をイメージして図示していきます。
始めは全く範囲が分割されていない状態からスタートします。

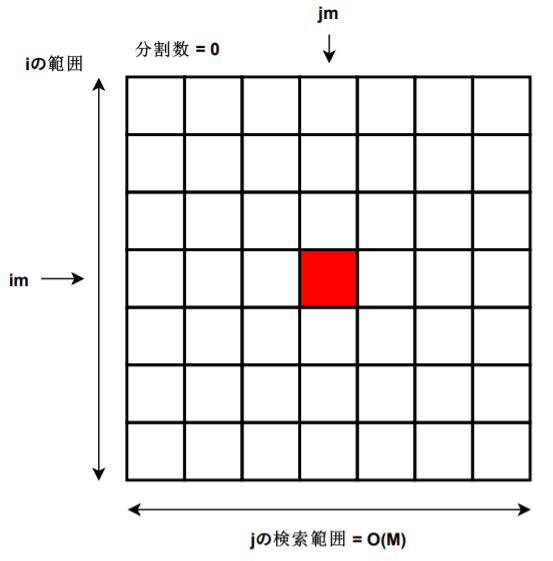
範囲が分割されていない初期状態

擬似コードにあったように、 の範囲の中心の について、 を最小にする を を全探索して求めます。この操作は明らかに 時間です。
次に一段階範囲を分割した(一段階再帰した)状態について見てみます。

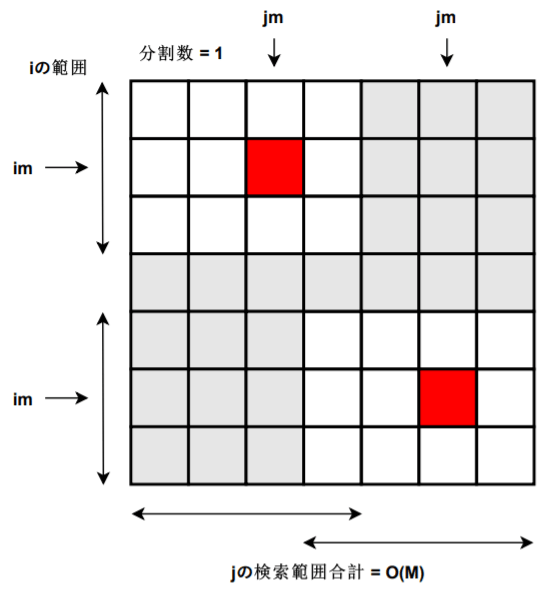
一段回分割した状態

分割されたそれぞれの範囲で の計算が行われます。この時行われる2つの の全探索について、探索範囲の重複を無視するとやはり合計で 時間の計算になっていることが分かります。
さらに分割して、

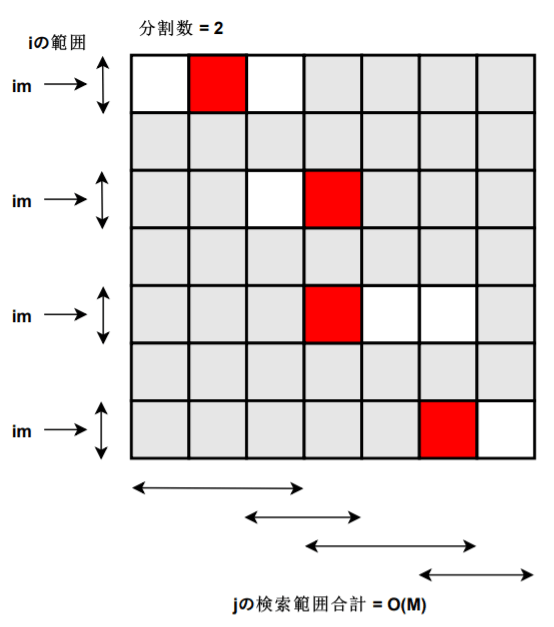
分割した範囲で計算

区間は4つに分かれましたが、やはり重複を無視して見ると の計算は合計 時間で収まっています。そして、これらの分割は、を毎回半分づつにしているため、最大 回しか起こりません。
各分割で無視された重複箇所の合計は 個になることに注意すると monotone minima のアルゴリズムは、全体 時間になることがわかります。
これは 時間からの高速化に成功しています。

まとめ

今回は最適化問題を解くシンプルな高速化手法 monotone minima について説明しました。

monotone minima はシンプルながら強力な手法で、動的計画法への興味深い応用も存在します。

いずれ他の記事でそちらにも触れていけたらと思います。ありがとうございました！

参考リンク

週刊 spaghetti_source / Totally Monotone Matrix Searching (SMAWK algorithm)
Kyopro Encyclopedia of Algorithms / Monotone minima
動的計画法高速化テクニック（オフライン・オンライン変換)