この間、反転数が関係する問題がうまく解けなくて悔しい思いをしたので、技術ブログでアルゴリズム連載企画ができたのを機に、反転数について考えてみたいと思います。

反転数の定義

数列に対して、かつを満たす組(i, j)の個数を、この数列の反転数(inversion number)という。

例えば、数列2, 4, 1, 3, 5の反転数を考えましょう。とするとかつなので（数列のインデックスはから始まるものとします）、これは条件を満たす組の1つです。が条件を満たすので、反転数は3です。

感覚的には、「数列がソートされている状態にどれくらい近いか・遠いか」を表す指標と言えるでしょう。

なお、反転数は転倒数という名前で呼ばれることもあります。

反転数と隣接互換の関係

今回知りたいのは、反転数と隣接互換によるソート回数の関係です。

先の2, 4, 1, 3, 5 という数列に対して、隣同士の要素の交換を繰り返してソートすると、2, 4, 1, 3, 5 → 2, 1, 4, 3, 5 → 2, 1, 3, 4, 5 → 1, 2, 3, 4, 5 と3回の交換でソートすることができます。この必要な交換回数は、実は反転数に等しい値です。分かってしまえばそれほど難しくないのですが、それほど自明でもないので少し難しいですね。今回証明を考えてみました。

補題：数列の反転数は、その数列をバブルソートでソートするときの交換回数に等しい。

証明：数列の反転数をとおく。バブルソートによる要素の交換は、逆順のものを正しい順に直す操作である。またこの交換は隣接要素間で行われるので、操作の前後の反転数を考えると、交換された要素だけが影響を受ける。したがって、操作によって反転数は必ず1だけ減少する。また定義より、ソートされた数列の反転数は0である。したがって、 $交換回数$ なので、は交換回数に等しい。

バブルソートのアルゴリズムについてはAIZU ONLINE JUDGEのページなどをご参照ください³。

命題：数列の反転数は、その数列を隣接要素を交換することによってソートするときの最小の交換回数に等しい。

証明：1回の隣接要素の交換によって、反転数は高々1しか減少しない。したがって、最初の反転数からソート済みの状態（反転数が0）にするには、最小でも回の交換が必要である。そして補題より、バブルソートを実行すると回の交換でソートすることができる。以上より、最小の交換回数は回である。

なお、最小回数を達成するために、必ずしもバブルソートを使う必要はありません。例えば、「一番小さい要素を探して、一つずつ前と交換していって一番前に移動させる。次に、残りの要素の中で一番小さい要素を探して、一つずつ前と交換していって前から二番目に移動させる……」という方式でも大丈夫です。

分割統治法による反転数の求め方

さて、反転数を求める方法について考えてみましょう。

もっとも単純な方法は、全てのペアについて1つずつチェックする方法で、計算量はとなります。

これよりも高速な解法として、Binary Indexed Tree（BIT）を用いた解法があります。「プログラミングコンテストチャレンジブック [第2版]」p.162に載っているほか、転倒数[いかたこのたこつぼ] が詳しいです。計算量はです。

しかし実は、アルゴリズム関連の他の本に載っている「反転数の求め方」は、BITによるものではありません。

アルゴリズム本の大著である「アルゴリズムデザイン」で反転数の求め方があるのは、「分割統治法」の章の中です。

分割統治法……! アルゴリズムの授業では必ず習うけど、実際にはなかなか使わないやつ……!

私自身の競技プログラミングの経験を振り返っても、分割統治法を組んだ覚えはありません。この機会に書いてみましょう。（分割統治法とは何か、という話は割愛します。分割統治法を使うアルゴリズムとしてはマージソートが有名なので、適宜調べてみて下さい。）

分割された小問題を統合する部分が重要ですので、この部分だけを取り出して書き直してみましょう。

数列AとBがある。AとBはソートされた長さN/2の数列である。これに対し、「AとBをつなげた数列をソートした数列Cを求めたい。同時に、a A, b B, かつ a > bとなる組の個数も求めたい。

反転数を求める上で数列を同時にソートすることは必須ではないので、上記の問題中にソートの話が出てくるのはやや不思議です。直観的には「バラバラな順番だったら高速に求めづらいから、余計な計算量をかけずにソートできるなら同時にソートしておいた方が後でやりやすいだろう」というところでしょうか。

さて、上記の問題に対するの解法を考えます。

数列AとBのそれぞれの先頭にポインターを置き、それを右にずらしながら小さい方の数字を数列Cに加えていくことで、ソート済みの数列を得ることができます（マージソートのときと同じです）。

あとは反転数を求めれば問題は解決です。これは、Bの要素を数列Cに加えるときに、残っているAの要素数を足し上げていけば良いです（下図を参照ください）。これにより、一つずつ数えることなく、反転数を短い計算時間で求めることが可能になります。

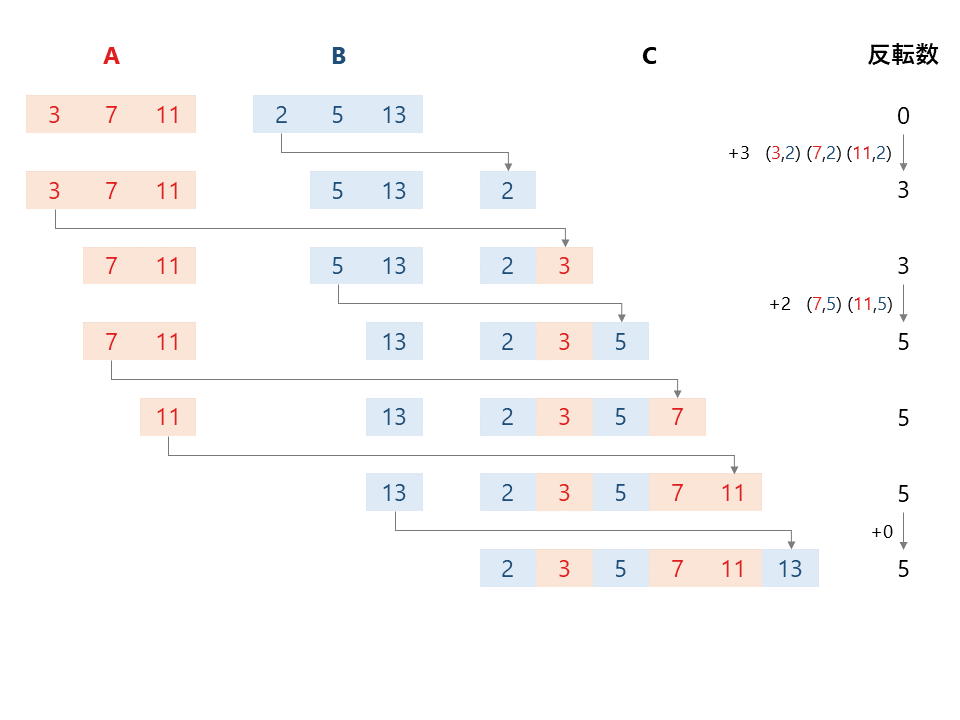
以上を踏まえてソースコード（Python）を書いてみましょう²。

def merge_and_count(list_a, list_b):
    len_a = len(list_a)
    len_b = len(list_b)
    idx_a = 0
    idx_b = 0
    count_inversion = 0
    merged = []

    # リストの両方が空でないとき
    while idx_a < len_a and idx_b < len_b:
        if list_a[idx_a] < list_b[idx_b]:
            merged.append(list_a[idx_a])
            idx_a += 1
        else:
            merged.append(list_b[idx_b])
            idx_b += 1
            # count_inversionを、Aの残っている要素数の分だけ増やす
            count_inversion += len_a - idx_a

    # リストの一方が空になったら、他方のリストの残りを全て出力リストに加える
    if idx_a < len_a:
        merged += list_a[idx_a:]
    if idx_b < len_b:
        merged += list_b[idx_b:]

    return count_inversion, merged

def sort_and_count(lis):
    if len(lis) == 1:
        return 0, lis
    if len(lis) == 2:
        if lis[0] < lis[1]:
            return 0, lis
        else:
            return 1, [lis[1], lis[0]]
    else:
        # リストをほぼ2等分する
        half = len(lis) // 2
        list_first = lis[:half]
        list_second = lis[half:]
        inversion_first, sorted_first = sort_and_count(list_first)
        inversion_second, sorted_second = sort_and_count(list_second)
        inversion_while_merging, sorted_full = merge_and_count(sorted_first, sorted_second)

        return inversion_first + inversion_second + inversion_while_merging, sorted_full

# 例
print(sort_and_count([2, 5, 7, 13, 3, 11]))
# -> (4, [2, 3, 5, 7, 11, 13])

計算量はBITの場合と同じく、です。

なお、AとBの要素について全探索を行って組の個数を求めると計算量はとなり、反転数を求める全体の計算量もとなってしまいます¹。

分割統治法による反転数計算の特徴は、以下のようになります。

メリット：BITで計算するためには1～Nの数列の並び替えでなければならないが、分割統治法ではそのような制約は無く、任意の要素の数列で使える
デメリット：計算量としてはBITと変わらないが、再帰による関数呼び出しが発生するため、実際にかかる計算時間はBITよりも長くなる

参考文献

アルゴリズムデザイン | Jon Kleinberg, Eva Tardos

プログラミングコンテストチャレンジブック [第2版]　～問題解決のアルゴリズム活用力とコーディングテクニックを鍛える～ | 秋葉拓哉, 岩田陽一, 北川宜稔

1.計算量の厳密な解析は「アルゴリズムデザイン」p.196にあります。直観的には、「AとBに対して全部探索するのなら、結局もとの数列の全ての対を（分割統治法のどこかの段階で）一度ずつ見て判定しているから、計算量は」と言えます。 ↩
2.「アルゴリズムデザイン」中では「要素が1ならば分割せずに返し、2以上ならば分割する」としていますが、このコードでは2の場合でもわざわざ1個と1個に分割せずに値を直接計算しています。再帰呼び出しによる計算量増加が怖いので。 ↩
3.余談ですが、バブルソートを正確に理解しているか気になって調べましたが、「アルゴリズムデザイン」にも「アルゴリズムイントロダクション」にも索引で項目が立っていませんでした。「プログラミングコンテストチャレンジブック [第2版]」では一言説明があるのみでした。……バブルソートの扱い、不遇すぎませんか? ↩

反転数について、隣接互換との関係、分割統治法による数え上げ

反転数の定義

反転数と隣接互換の関係

分割統治法による反転数の求め方

参考文献