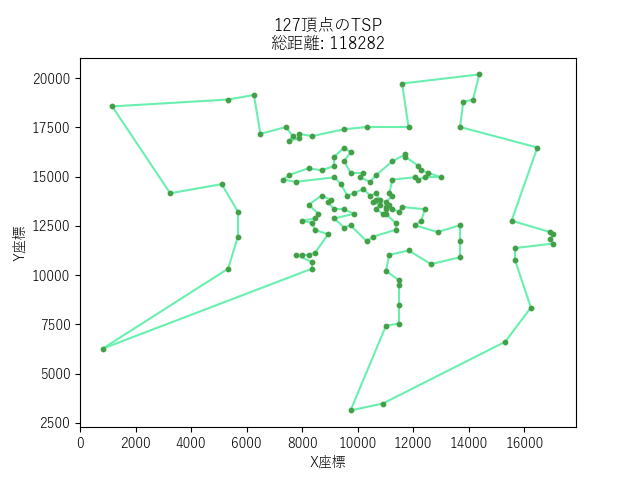
SAIGアルバイトの後藤です。業務では、アルゴリズムの知識を用いた既存処理の高速化やスケジュールの自動作成による業務の効率化を行っています。

配送計画問題など、最適化問題に属する社会課題は、部分問題に巡回セールスマン問題(TSP: Travelling Salesman Problem)を含むことが少なくありません。したがってTSPの基本的なアプローチを知っていることは重要です。TSPは組合せ最適化の代表的な問題として古くから様々なアプローチが試みられており、本記事は専門家の方にとっては既知の内容だと思いますが改めて紹介します。この記事では、2/3-optの焼きなまし法(SA: Simulated Annealing)より良い解法として2/3-optの反復局所探索法(ILS: Iterated Local Search)を紹介します(競技プログラマへ: TSPは焼きなましより山登り + Kickが良いという話をします)。

TSPにおいて特に良いとされているILSには次の2つがあります[1]。

• Lin-Kernighan heuristic ILS
• 2/3-opt ILS

本記事では、この内の2/3-opt ILSについて紹介します。

目次

• 導入
  • 巡回セールスマン問題(TSP: Travelling Salesman Problem))
  • TSPの種類
  • 現実の問題
  • 異なるアルゴリズムの結果を比較
• アルゴリズム
  • 2/3-opt
  • 局所探索法(LS: Local Search))
  • 反復局所探索法(ILS: Iterated Local Search))
  • Double-Bridge
  • 焼きなまし法(SA: Simulated Annealing))
  • 2-opt ILS
  • 2-optの実装上の工夫
  • その他の工夫
• 実験方法
  • 比較方法
  • 使用したテストケース
  • 使用した言語
• 実験結果
• さいごに

導入

巡回セールスマン問題(TSP: Travelling Salesman Problem)

TSPは次のような問題です。

個の頂点 がある。頂点 間には辺 が張られており、距離 が定められている。
このとき、巡回路(長さ の順列 を用いて と表せるような辺集合)のうち、距離の総和が最も短いものを求めよ。

巡回路は、頂点 から出発して、他のすべての頂点をただ一度だけ通り頂点 に戻ってくる経路と解釈できます。図に表すと、次のようになります。

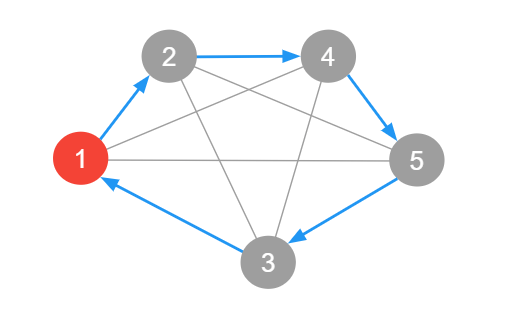
丸が各頂点です。矢印が巡回路を表しています。
頂点 に戻ってこないようなバリエーションも存在しますが、同様のアプローチが有効です。

最も距離の短い解(巡回路)を愚直に求めようとすると組合せ爆発が起こり、頂点数が多くなると現実的な時間内で解を見つけることができません。そこで、なるべく総距離の短い解(近似解)を一定時間内に見つけることを考えます。このようなアルゴリズムをヒューリスティックアルゴリズムと言います。短時間でより良い解が見つかるアルゴリズムが良いヒューリスティックアルゴリズムと言えます。この記事では、TSPのヒューリスティックアルゴリズムとしてよく紹介されるアプローチを実際に用いて、検証・比較を行います。

TSPの種類

TSPは距離の制約によりいくつかの種類があります。基本的な制約は次の3つです。

• Metric: 三角不等式 が成り立つ。
• Symmetric: 頂点 から への距離と、頂点 から への距離が等しい。すなわち、 が成り立つ。
• Euclidean: 頂点間の距離が2次元ユークリッド空間上の距離になっている。すなわち、が成り立つ。ただし、 は頂点 の 座標、 は頂点 の 座標を表す。

EuclideanならMetricかつSymmetricです。また、Symmetricでない場合をAsymmetricと言います。
この記事ではSymmetricが成り立つTSP、すなわちSymmetric TSPのみを考えます。なお、Asymmetric TSPは適切な変形によりSymmetric TSPに帰着できます[2]。

現実の問題

TSPは現実では、次のような問題として現れます。

• 郵便物配達のルート最適化
• 作業スケジューリングの最適化

図1が郵便物配達時のルートを表しているとすると、頂点 が郵便局などの配達拠点、頂点 が配達先に該当します。頂点間の距離は移動にかかる時間などでも良く、その場合はなるべくすべての配達先を訪れてなるべく早く帰ってくるルートを探す問題になります。

作業スケジューリングの最適化は一見するとTSPには関係なさそうですが、次のような場合TSPと見なせます。

個の作業 がある。作業 を行った後に作業 を行うと、作業 の準備には, 分かかる。また、何も作業を行っていない初めの状態を作業 とし、同じく が定まっている。
このとき、作業 から始めて、すべての作業をただ一度だけ行い作業 に戻ってくる順番のうち、最も準備時間が短いものを求めよ。

イメージとしては、作業 は作業前の片付いた状態で、その状態から作業 の準備にかかる時間が 分です。そこからすべての作業を終えて、また作業前の状態に片付けるための最適な順番を求めるのが、上記のスケジューリング問題になります。

異なるアルゴリズムの結果を比較

異なる3つのアルゴリズムで127頂点のTSPを解いたときの巡回路をビジュアライズしました。

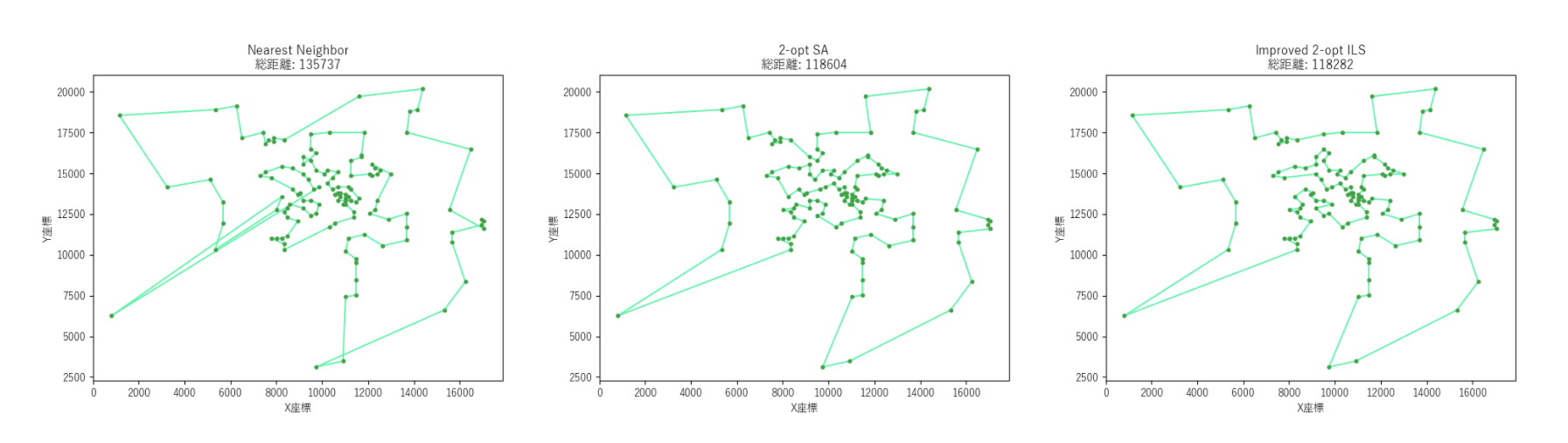
左からNearest Neighbor(貪欲法)、2-opt SA、2-opt ILS(今回紹介する手法)です。それぞれの巡回路の総距離は135737, 1186034, 118282となっています。2-opt ILSの巡回路は最適解で、最も総距離が短い巡回路です。
Nearest Neighborは、頂点 (またはランダムな頂点)からまだ訪れていない頂点のうち最も近いものから訪れることを繰り返す単純な手法ですが、最後の方に余った頂点に訪れなければいけないため、明らかに効率が悪くなっている経路があります。
2-opt SAと2-opt ILSの違いは分かりにくいですが、よく見ると中央付近のルートが異なります。

アルゴリズム

2/3-opt

2-opt(3-opt)はある巡回路から2つ(3つ)の辺を削除して2つ(3つ)の辺を繋ぎ直すことを改善ができなくなるまで繰り返すアルゴリズムです。
2-optは次の図のようなイメージです。図では頂点番号を省略しています。

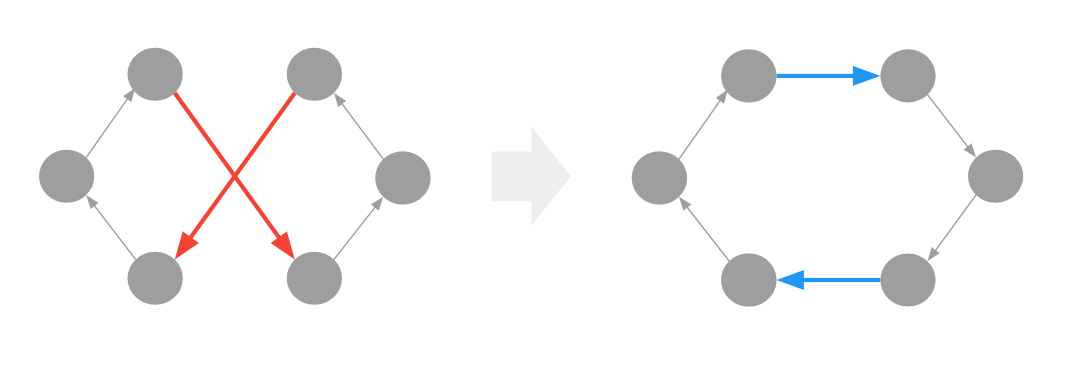
左の順回路から赤い2つの辺を削除して、その後に青い辺で辺が削除された頂点を繋ぎ直しています。これにより、巡回路が効率的になっています。このような変更をどの辺の組に対して行っても改善ができなくなるまで行うのが2-optです。改善できないような組に対しては変更を行いません。3-optの場合は、3つの辺を削除し3つの辺を繋ぎ直す組み合わせをすべて試し、最も距離が短くなるような繋ぎ方に繋ぎ直します。

一般に、 個の辺を削除し 個の辺を繋ぎ直して改善することを改善ができなくなるまで繰り返すアルゴリズムを-optと言います。

局所探索法(LS: Local Search)

ILSを紹介するにあたり、まずLSを紹介します。

現在の解 から、ある操作を行って得られる解の集合 を の近傍と言います。LSは、この近傍の中から よりも良い解、すなわち となるような に遷移し続けて、遷移ができなくなるまで繰り返す手法です。2-optもLSの一種であり、近傍 は巡回路 から2本の辺を繋ぎ直して得られる巡回路の集合です。
これ以上改善が行えないような解 、すなわち となるような が存在しないような を局所解と呼びます。

def local_search(x):
    while True:
        updated = False
        for x2 in sigma(x):  // xの近傍をすべて見る
            if score(x2) < score(x):
                x = x2
                updated = True
                break
        if not updated:
            break
    return x

反復局所探索法(ILS: Iterated Local Search)

LSでは局所解に達したときに必ずそれが最適解であるという保証は通常ありません。そこで、LSで局所最適解に到達した場合にKickまたはPerturbationと呼ばれる遷移[3]により局所解を脱出し、再びLSを適用することにより別の局所解へと遷移することを期待する手法がILSです。そのためKickはLSでまた同じ局所解へと到達しにくい遷移である必要があります。しかし一方で、できるだけ変更の小さな遷移が良いとされています。現在の比較的良い解を壊しすぎてしまうと、ランダムに解を作成してLSを適用するのと変わらなくなってしまうためです。

def iterated_local_search(x):
    x_global = x
    for i in range(num_iterated):
        x = x_global
        x = kick(x)
        x = local_search(x)
        if score(x) < score(x_global):
            x_global = x

    return x_global

Double-Bridge

TSPで近傍を2/3-optにする場合、KickはDouble-Bridgeという遷移が良いとされています[3]。
Double-Bridgeでは、次のように赤い辺を4つ削除し、青い辺で繋ぎ直します。

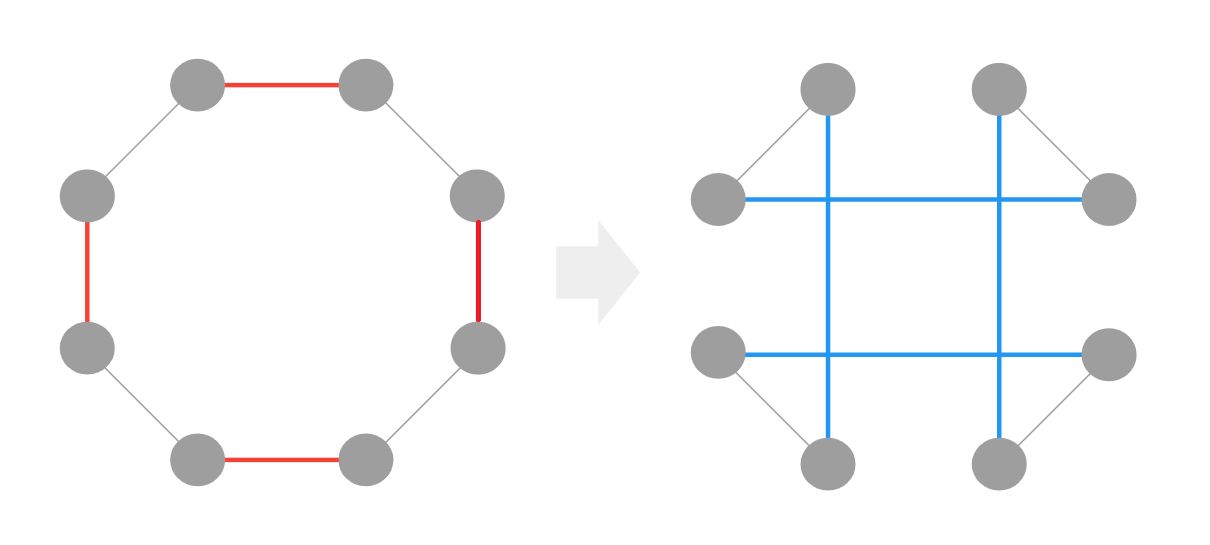
一見、2-optを2回適用することで同じ遷移ができるような気がしますが、途中で巡回路を2つに分離してしまうため、2回では不可能です。また、辺を変える本数も4本と2/3-optにない遷移の中で最低の本数であるため、元の解からの変更は最小限です。そのため、2/3-optのKickとしてDouble-Bridgeは適しているとされています。本来Double-Bridgeはこの記事では紹介しないLin-Kernighan heuristicの近傍に含まれないような最小の変化から来ています。

焼きなまし法(SA: Simulated Annealing)

SAは確率的に近傍から解 を選びます。 である場合は に遷移し、の場合はスコアの悪化具合と実行時間やループ回数に応じて確率的に遷移します。スコアが悪化するほど遷移する確率は低く、実行時間が長い/ループ回数が多いほど遷移する確率は低くなります。
記事にある2/3-opt SAは、近傍を2/3-optの近傍にしたものです。2-opt(3-opt)で削除する辺を2つ(3つ)ランダムで選び辺を繋ぎ直して遷移をします。

温度などSAの詳しいことについてはこの記事では説明しません。

SAの擬似コードです。

def simulated_annealing(x):
    temp = start_temp  // 初期温度の設定
    while elapsed() < time_limit:  // 一定の時間ループを回す
        x2 = choose_from_sigma(x)  // 近傍からランダムで遷移先を選ぶ
        diff = score(x2) - score(x)
        if diff < 0 or prob(diff, temp):
            x = x2
        temp = update_temp(elapsed(), time_limit)  // 温度の更新

2-opt ILS

今回紹介する手法は、2-opt ILSです。LS部分を2-optにして、KickをDouble-Bridgeにします。
今回の手法ではランダムに選んだ4本の辺を使ってDouble-Bridgeを行います。この時、選ぶ4辺に制約や遷移後の解の総距離による遷移の制限はありません。完全にランダムで1度だけDouble-Bridgeを行ってから2-optによるLSを行うことを繰り返します。

擬似コードは次の通りです。

def iterated_local_search(x):
    x_global = x
    for i in range(num_iterated):
        x = x_global
        x = double_bridge(x)
        x = two_opt(x)
        if score(x) < score(x_global):
            x_global = x

    return x_global

2-optの実装上の工夫

頂点が 個の場合、削除できる辺が 個ありそこから2つ選ぶので、2-optの近傍は全部で 個あります(同一視の仕方にもよります)。しかし、スコアが改善できる解 があるかどうかを調べるのに、実はすべての近傍を見る必要はありません。この工夫により、2-opt ILSの性能は飛躍的に良くなります。

今、巡回路中に および があるとします( は相異なります)。

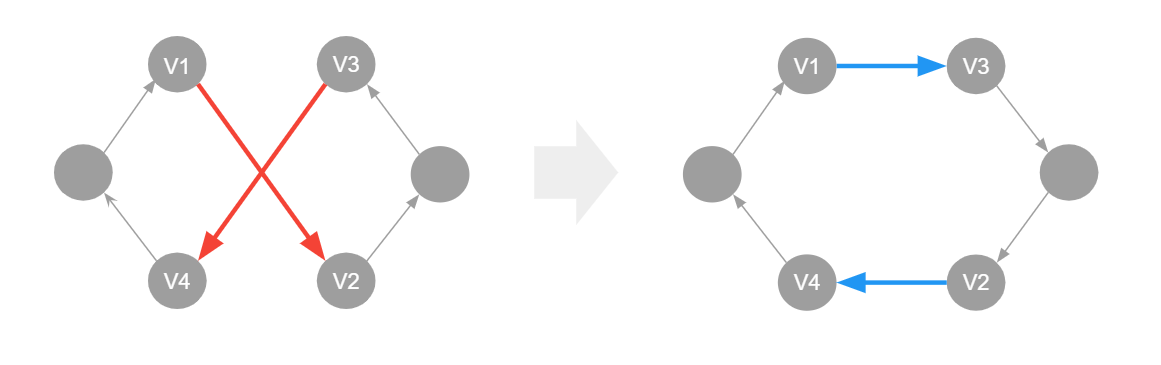
このとき、2-optで2つの辺 を繋ぎ変えてスコアが良くなるには、次の条件を満たしている必要があります。

この条件は次の条件を2つとも満たしている場合、成り立ちません。

各不等式の和を取ると になるからです。

したがって、2-optで2つの辺 を繋ぎ変えてスコアが良くなるには、次の条件のどちらかを満たしている必要があります(十分でない)。(条件1)

以上から、2つの条件のどちらかを満たしている辺をすべて調べ上げれば、現在の巡回路から2-optで改善できるかどうかが分かります。
具体的には次の通りです。

今、辺 を削除する1つ目の辺とします。この時、削除する2つ目の辺の候補として次の条件のうちどちらかを満たす を調べれば十分です。

1つ目の式は になる場合、2つ目の式は になる場合です。2つ目の式ではSymmetricであることを使いました。
つまり、 よりも から近い頂点が の候補に、 よりも から近い頂点が の候補になります。 か のどちらかが決まればもう一方も決まることに注意してください。

これを巡回路中の全ての辺に対して行えば、条件1を満たす全ての辺の組を探索できます。

上の条件を満たす頂点を効率的に探すには、あらかじめ各頂点から近い順に他の頂点のリストを持っておけばよいです。これは、構築時に で処理することが可能です。

同様の工夫を3-optに対して行うことも可能です。

[4]のHow to Make 2-Opt and 3-Opt Run Quicklyに条件1のうち片方だけ見れば良いと書いていたので、片方だけ見る実装も実験に加えました。しかし、条件を片方だけ見れば良いというのは嘘で、例えば1つ目の条件だけを見ていると次のようなケースを見逃します(もし間違いであればご指摘お願いします)。

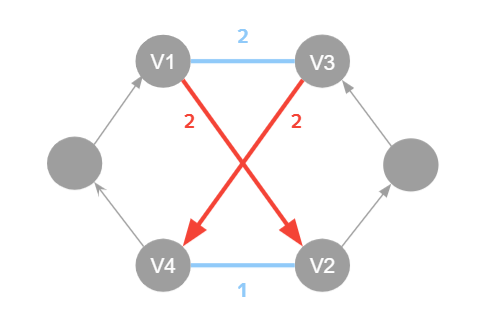
その他の工夫

その他にも、頂点 から最も近い 点のみを探索する、辺を削除した頂点の近くの頂点のみを探索するなどの高速化方法がありますが[4]、今回は実装していません。

実験方法

比較方法

比較するアルゴリズムは次の通りです。実行時間と発見した解の総距離を比較します。

• Nearest Neighbor
• 2-opt LS (実装上の工夫なし)
• 3-opt LS (実装上の工夫なし)
• 2-opt SA
• 3-opt SA
• 2-opt ILS (実装上の工夫なし)
• 3-opt ILS (実装上の工夫なし)
• Improved 2-opt ILS (実装上の工夫あり)
• Improved 2-opt ILS one-side (実装上の工夫あり) (条件1のうち片方の条件のみを見る)

LSは局所解に達するまで実行し局所解に達したときの時間を実行時間としています。
SA/ILSは10秒間実行した時の解を出力します。Kick + LSの実行が終わったタイミングで時間制限を過ぎていた場合、そこまでに発見した解を出力とします。したがって、実行時間が10秒を過ぎる場合があります。

使用したテストケース

TSPLIBのSymmetric TSPインスタンスの中から、EDGE_WEIGHT_TYPEがEUC_2DかEXPLICITであり頂点数が5000以下のものをすべて選び実験を行いました。EDGE_WEIGHT_TYPEはグラフの辺の重みの指定の仕方です。EUC_2Dは各頂点の位置が2次元ユークリッド空間上の点として与えられ、頂点間の距離はユークリッド距離を整数に丸めたものです。EXPLICITは頂点間の距離が明示的に与えられます。EDGE_WEIGHT_TYPEは他にもありますが、今回の実験ではこの2つのみを使用しました。理由は、インスタンスを読み込むプログラムを作る時間的コストと使用できるインスタンスの個数の兼ね合いです。頂点数の制約は実行時間から来ています。特に、3-optは破滅的な時間がかかります。

使用した言語

Javaを使って実験を行いました。

備考

巡回路は、頂点番号の動的配列として表現しました。この場合、2-optや3-optでは区間反転操作を行う必要が出てきますが、線形時間かけて愚直に行っています。
SAの温度管理には、頂点間の距離の平均を とおき、初期温度を 、最終温度を とする指数スケジューリングを用いています。

実験結果

最も良いスコアを太字にしています。最もスコアが良い手法が複数ある場合は、その中で計算時間が最も少ない手法のスコアと計算時間を太字にしています。また、optimumはそのインスタンスの最適解であり、見つかった解が最適解である場合はoptimumの列を太字にしています。
また、3-optなど実行が10秒以内に終わらなかったものは太字にする処理の対象外としています。機械的に実行時間が11000msより大きい場合は対象外としています。

※ 追記(2021/12/06)

• 解と最適解のスコアの比(score / optimum)を表に追加しました。
• 行の順番を頂点数の少ない順にしました。

次に2-opt SAとImproved 2-opt ILSで見つかった解が最適解の何倍であるかをプロットした図を示します。

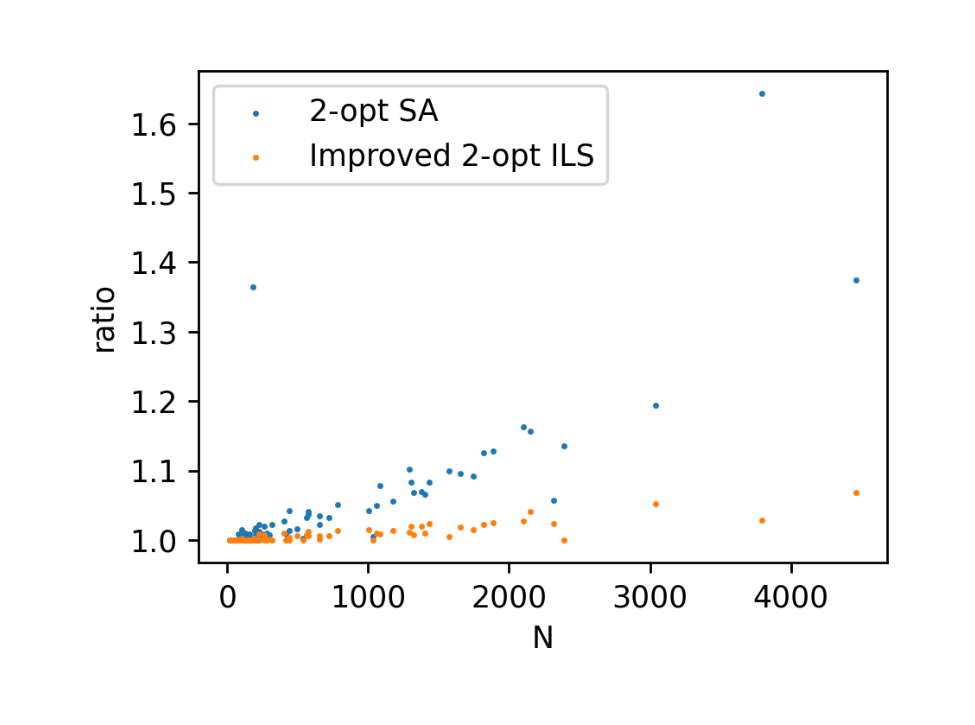
横軸が頂点数、縦軸が見つかった解の総距離/最適解の総距離です。点がグラフの下にプロットされているほど最適解に近く、良い解が見つかっています。

Improved 2-opt ILSの条件を2つとも見た場合と1つだけ見た場合の比較です。

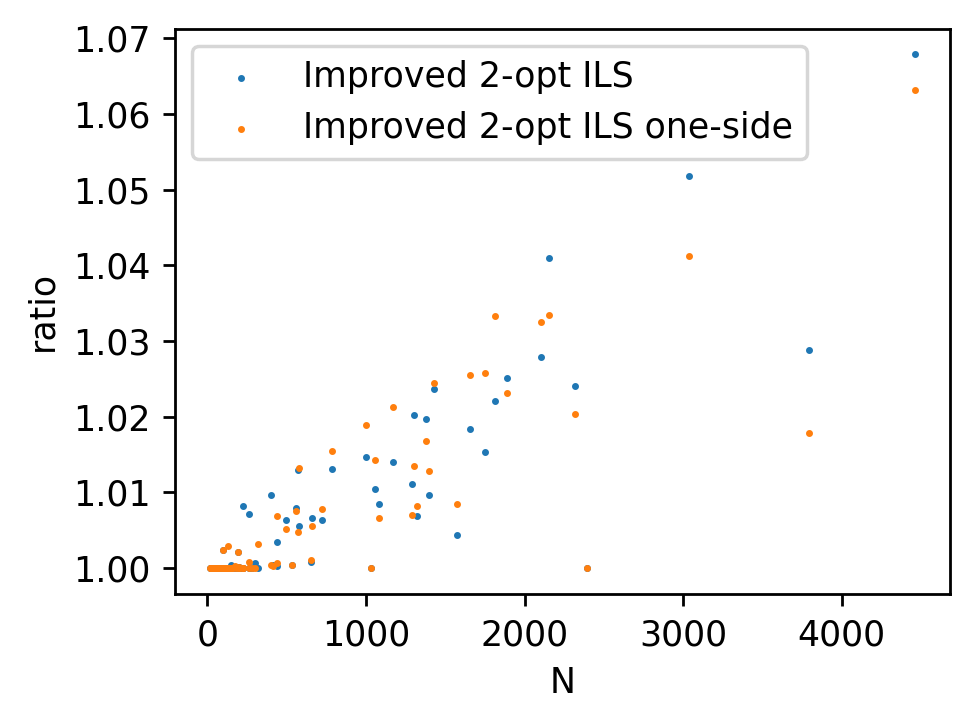
頂点数が多いインスタンスでは、片方の条件のみを見た方が良い解が見つかる傾向にありそうです。これは制限時間10秒では、片方の条件を見ずに多少改善を見逃すことよりも、多くの回数のKick + LSを行った方が良いからだと考えられます。

さいごに

多くの場合に単純な2-opt SAより2-opt ILSの方が時間内に良い解を出せることが実験から分かりました。
自分でTSPやTSPに類似した問題のソルバを書かなければならない場合はこの知識が役に立つかと思います。しかし、自分で書く必要がなくライセンス条件を満たす場合は既存のヒューリスティックソルバ[5]を使ったほうが圧倒的に性能が良く、手間もかかりません。
また、厳密に解くソルバも存在します。TSPを厳密に解くのは数十頂点ですら難しいと思われがちですが、このソルバで厳密に解けている数万頂点の問題もあります[6]。各インスタンスの最適解がどうして分かるのか疑問に思った方もいると思いますが、このような厳密に解くソルバによって最適解が求まっています。

参考

[1] Hong, Inki, Andrew B. Kahng, and Byung-Ro Moon. 1997. “Improved Large-Step Markov Chain Variants for the Symmetric TSP.” Journal of Heuristics 3 (1): 63–81. https://doi.org/10.1023/a:1009624916728.

[2] Johnson, David S., Gregory Gutin, Lyle A. McGeoch, Anders Yeo, Weixiong Zhang, and Alexei Zverovitch. 2007. “Experimental Analysis of Heuristics for the ATSP.” In The Traveling Salesman Problem and Its Variations, edited by Gregory Gutin and Abraham P. Punnen, 445–87. Boston, MA: Springer US. https://doi.org/10.1007/0-306-48213-4_10.

[3] Martin, Olivier, Steve W. Otto, and Edward W. Felten. 1992. “Large-Step Markov Chains for the TSP Incorporating Local Search Heuristics.” Operations Research Letters 11 (4): 219–24. https://doi.org/10.1016/0167-6377(92)90028-2.

[4] Johnson, D., and L. A. McGeoch. 1995. “The Traveling Salesman Problem: A Case Study in Local Optimization.” https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.70.7639&rep=rep1&type=pdf.

[5] K. Helsgaun. 2019. “LKH-3” http://webhotel4.ruc.dk/~keld/research/LKH-3/

[6] “Concorde TSP Solver” https://www.math.uwaterloo.ca/tsp/concorde.html