はじめに

本記事は、2021/10/23(土)に行われたPG Battle 2021の参戦記です。

フューチャーから3人1組で3チーム参加し、なんと企業の部6位に入賞できました！！

本記事を通じて、競技プログラミングに興味のある方が少しでも増えると良いなーと思っています！

自己紹介

2021年7月フューチャー新卒入社の栗城です。競プロ歴は2年弱（就活期の終盤に始めました）、

問題を解くのが大好きで、毎週末AtCoderのコンテストに参加しています。2022年2月からOCV（フューチャーの競技プログラミング部）の部長を務めさせていただいています。

競技プログラミングとは

競技プログラミングは与えられた問題を好きなプログラミング言語で解く競技です。略して「競プロ」と言います。日本ではAtCoderというコンテストサイトが有名で、毎週末コンテストが開催されています。

初級レベルでは求められた処理をそのまま実装すれば正解できる問題が多く出題されるので、

プログラミングに慣れたい
新しいプログラミング言語を習得したい

という方には非常におすすめです。

コンテストとかは興味ないけど気軽にアルゴリズムの練習をしてみたいという方には、アルゴ式というサイトがあります。プログラミングを通して簡単な算数・アルゴリズム・統計などを基礎的なレベルから学ぶことができ、新しい言語の習得にも役立ちます。

一方コンテストにおいては、上位になればなるほどアルゴリズム力・思考力・数学力を極める戦いとなります。

アルゴリズムを駆使するような仕事でない限り実務からはだんだん離れていきますが、それでも

問題の本質を見抜く力
複雑なロジックを最後まで考え抜く思考体力
思いついた解法を素早く正確にコードに落とし込む実装力

このあたりは実務にも大いに役立つところだと思っています。

どんな問題が出るのか気になる方は、今回PG Battleで出題された問題をこの記事の後半で紹介していますので、
ぜひ見てみてください！

PG Battleとは

毎年秋に開催される競プロのチーム戦で、ルールはこんな感じです。

同じ会社や学校の中で3人チームを組んで参加
3人で「ましゅまろ」「せんべい」「かつおぶし」の各4問セットを別々に解き、チームの合計点を競う
「ましゅまろ」 < 「せんべい」 < 「かつおぶし」の順に難しくなる（堅い方が難しい！）
合計点が同じ場合は、合計解答時間の短いチームが上位
企業の部・大学生の部・高校生以下の部のそれぞれで順位を競う

細かい参加方法やルール・注意点などは去年の体験記にあるので、気になる方は読んでみてください。

OCVでは毎年部内でチームを組んで参加するのが恒例となっており、今年は以下の３チームで参加しました。

例年より~~適当な~~個性の強いチーム名でした笑

犬もこもこ栗いがいが（※筆者のチームです）
Hello 猫 World!
あと一人足りない！行けたら行くチーム

コンテスト当日

私のチームは

ましゅまろ担当：baku1101
せんべい担当：marroncastle917
かつおぶし担当：yamad

の同期新人チームでした。
水青黄¹とバランスが取れたチームが組めたので、始まる前から上位狙えるかも？とは思っていました。

私は競プロのコンテストに普段から参加しているので、前年の過去問を解く以外に特に対策はしませんでした。PG Battle自体は初めてだったので、本番で使用するTOPSICというサイトから提出の練習などをして本番を迎えました。

本番では私が担当したせんべいは第3問までは比較的解きやすい問題でしたが第4問が非常に難しく、第4問を考えている間にタイムアップ！問題はこちらから見られます。

最後まで提出ボタンを押さなかったので、オンラインに保存していたコードが提出されたかどうか不安になりましたが、提出履歴を見るときちんと提出されており、一安心。

反省としては、時間いっぱいまで考え続けるのではなく、第4問にもっと早く見切りをつけて解答終了すべきでした。

点数が同じチームは3人の解答時間の合計で順位が決まるからです。チームの足を少し引っ張ってしまったので、この点は来年への教訓です。

結果発表

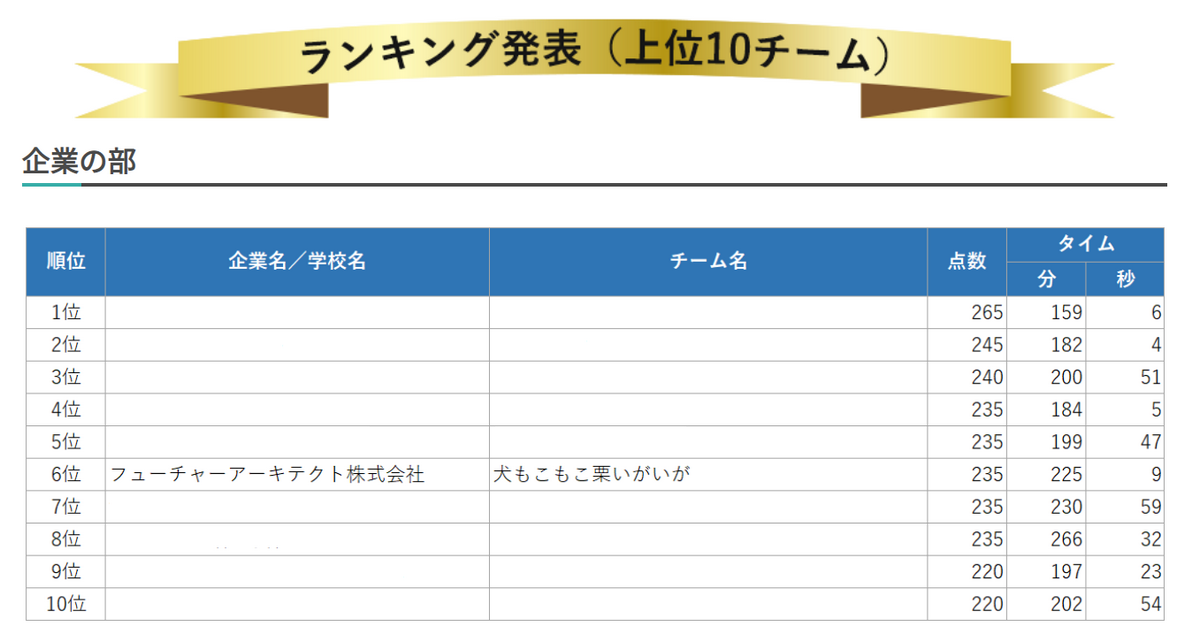
終了から数時間後に採点結果が発表され、以下のような結果でした。

ましゅまろ：100点（4問中4問正解）。
せんべい：65点（4問中3問正解）。
かつおぶし：70点（4問中3問正解）

3人とも取るべき問題をミスなく正解でき、ベストを尽くせたと言っていい結果になりました！

Twitterなどで感想を見る限り上位が期待できそうなことが分かったので、順位発表を楽しみに1週間過ごしました。

1週間後に結果発表があり、冒頭にも書いた通り企業の部194チーム中6位という成績を収めることができました！景品は上位3チームと10位以降の飛び賞しかないのでもらえませんでしたが、トップ10に入ると順位表に企業名が出るので、会社の名前を残せたことが何より良かったなと思っています。チームメイトに感謝です。

問題紹介

私が解いた「せんべい」の第3問「トーナメント表」の問題を紹介します。

この問題はアルゴリズムの知識は特に必要ないので、競プロ未経験の方もぜひ考えてみてください。

問題の全文はこちらから見られます。

読んでもよく分からなかった方のために、改めて説明します。

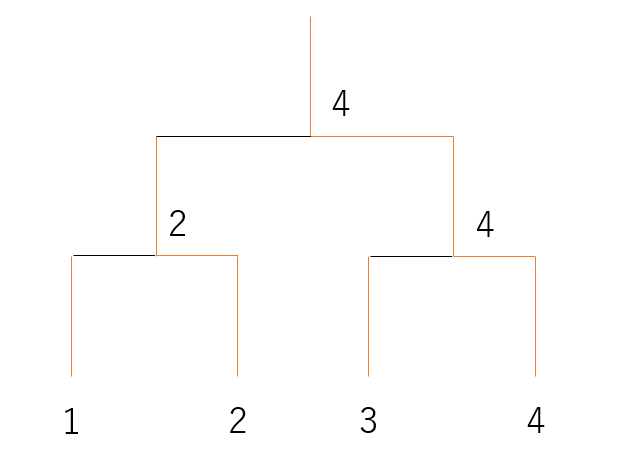
例えば、人１～４の４人がいたとして、とある組み合わせでトーナメント形式で対決した結果、

人１：ベスト４
人２：ベスト４
人３：ベスト２
人４：ベスト１

だったことだけが分かっているとします。

このとき、もしトーナメント上の人の並びが問題文中の図のようだったとしたら、各試合の勝敗を図のように決めれば人１～４がそれぞれ「ベスト４、ベスト４、ベスト２、ベスト１」になりますよね。

このように、適切に勝敗を定めれば与えられた順位を実現できるようなトーナメント表の人の並び方を出力するのがこの問題です。この例では「3,1,2,4」と出力すれば正解となります（他の正答もあり得ます）

競プロでは最適解を求める問題が多いのですが、この問題はそうではなく、条件を満たす解を何でもよいので1つ出力する形式です。このような問題を「構築問題」といい、理詰めのプロセスだけでなく「実験」や「ちょっとしたひらめき」が必要になることが多く、得意不得意がはっきりしやすいのが特徴です。

解説

さて、この問題はどう考えれば良いでしょうか。

まず、どう転んでも各順位を取る人数は決まっているので、人数の分布が違っていたらダメそうです。例えば、ベスト１（優勝者）やベスト２（準優勝者）が２人以上いたり、ベスト４が１人しかいないようなことはあり得ないため、そのような場合は-1を出力します。

一方、順位ごとの人数が適切な場合は工夫すれば上手くいきそうです。ここで人の並びを定めやすくするために、トーナメントの勝敗をこちらで決めてしまうことにしましょう。今回は、各対戦において右側の人が必ず勝つことにします。

つまり、の場合には以下のように対戦が進むことを仮定します。トーナメント表.PNG

図中の数字は人の番号ではなく、トーナメント上の位置が左から何番目かを表すことに注意してください。以後、この左から数えた位置を位置番号と呼ぶことにします。

実は、どのように勝敗を決めたとしても各順位の人数は変わらないため、適切な解を必ず構成できます。よって、勝敗は好きなように決めて良いのです。

勝敗さえ決めてしまえばあとは人を適切な位置に配置していくだけなのですが、実装をやりやすくするため、ここでは以下のような性質に注目します。

各対戦では位置番号が2で割り切れる回数が多い方が勝利している
位置番号が2で何回割り切れるかで最終順位が決まる

の例だと位置番号が2で割り切れる回数によって

2回：ベスト１（位置４）
1回：ベスト２（位置２）
0回：ベスト４（位置１，３）

のようになっています。
ピンと来ない方は、のトーナメント表を実際に書いてみると分かりやすいと思います。

この性質を一般化すると、

位置番号が2で割り切れる回数がちょうど回ならベスト

と表すことができます。さらに、ベストになるのは回勝利することと同値なため、

位置番号が2で割り切れる回数がちょうど回なら回勝利する

と言い換えればよりシンプルになります。また、この逆も成り立ちます。

2で割り切れる回数だけ勝利するというのは面白い性質ですね。

以上より、与えられた順位情報から各人が何回勝利したかを求め、

勝した人を2でちょうど回割り切れる位置に配置

するように実装すれば、正解が得られます。

計算量はとなり、であることから回程度の計算で収まるので、実行時間制限2秒に余裕をもって間に合います。

以下は、Pythonでこの方針を実装してみたものです。本番で私が提出したコードを可読性を上げるために改良し、コメントをつけてみました。ジャッジで確かめていないので間違いがないとは言い切れませんが、方針は合っているはずです。

Part１　入力を受け取る

N = int(input())                    # トーナメントの深さ
A = list(map(int, input().split())) # 各人の順位を並べた配列
M = pow(2,N)                        # 参加人数

pow(2,N)は2の乗です。

Part２　勝利数ごとに人の番号を記録

rank_to_win = {pow(2,i) : N-i for i in range(N+1)} # 「ベストa」を「勝利数」に変換する辞書（javaでいうmap）
people_nums = [[] for w in range(N+1)]             # w勝した人の番号を記録する配列
for i,a in enumerate(A):        # 配列Aの要素aを0始まりのインデックスiとともに繰り返す
    num = i+1                   # 人の番号
    w = rank_to_win[a]          # num番の人の勝利数、ベストaを勝利数に変換
    people_nums[w].append(num)  # w勝した人の番号を記録する配列にnum番を追加

勝した人の番号を_に記録します。

Part３　トーナメント上に実際に人を並べる

# 答え（トーナメントに並べる人の番号）の配列
ans = [0]*M

# 0勝からN勝まで繰り返し
for w in range(N+1):
    # w勝した人のトーナメント上の位置番号(1-index)を表す配列
    positions = list(range(pow(2,w), M+1, pow(2,w+1)))

    # w勝した人の人数が位置番号の数と合わなければ-1を出力して終了
    if len(people_nums[w]) != len(positions):
        print(-1)
        exit()

    # トーナメント上の位置（pos）にnum番の人を配置（同じ勝利数の人の中では順不同）
    for pos, num in zip(positions, people_nums[w]):
        ans[pos-1] = num

# 答えを出力
print(*ans)

本質パートです。このパートで答えまで出力しています。
Python特有の記法である

list(range(pow(2,w), M+1, pow(2,w+1)))

では、から始めて間隔でまでのリストを作っており、でちょうど回割り切れる数を全列挙しています。
の場合はとなります。

解説は以上です。いかがでしたでしょうか。

この問題は他にも様々なやり方があるので、余裕があれば考えてみてください。解の構成自体はそこまで難しいものではありませんが、どう実装するかが問われる問題だったかなと思います。

あと、問題の作りが自然というか実際自分でも考えたくなりそうな問題設定で、個人的にはとても好きな問題でした。

公式が出しているpython, C++, javaによる解答例や、AtCoder社長による解説動画もあるので参考にしてみてください。

感想

私自身は競プロで入賞するのが初めてだったので、とてもうれしかったです。私のように個人では到底最上位は狙えないような実力でも、同じ企業内で粒を揃えられれば上位を狙えるのがPG Battleの魅力だなと思います。

それから、去年よりも全体的に面白い問題が多く解きがいがありました。

意外と競プロの公式チーム戦は数が少ないので、このような機会を毎年提供してくださる主催者の方々にとても感謝ですし、レベルが近いメンバーで比較的簡単にチームが組める社内の競プロerのレベルの高さにも恵まれているなと感じました。

おわりに

最後までお読みいただきありがとうございました！競技プログラミングに少しでも興味を持っていただけたでしょうか。

OCV（フューチャーの競プロ部）では灰色からレッドコーダーまで様々なレベルの方が在籍しています。

まだ部長になったばかりなので本格的な活動はこれからになりますが、気軽に教え合ったり情報交換したりできる環境を作っていく予定です。

興味のある方はぜひお声がけください！

1.色はAtCoderにおける強さを表していて、灰,茶,緑,水,青,黄,橙,赤,自由色の順に強くなります。詳しくはこちらを読んでみてください。各色がどれぐらいの実力なのかについてAtCoderの社長が詳しく書いてくださっています。 ↩

PG BATTLE 2021 参戦記