本記事は「秋のブログ週間2023」2週目の記事です。

はじめに

旅行をするときや引っ越しをするとき、周辺の商業地域や、観光地にアクセスのよい「地の利」のある場所を探したいですよね？

「地の利」がある場所を探すには、インターネットで調べるか、長らくその地域に住んでいて土地勘のある人に聞くのが一般的ではないでしょうか。

今回は、数理的なアプローチで「地の利」の良い場所を見つける方法を紹介します。

「地の利」とは”地形や土地の位置が、ある事をするために有利な条件を備えていること”です（引用:コトバンク）。本記事では単純に、他の場所へ行きやすい「アクセスが良い場所」のような意味で使っております。

本記事は都市と地域を数理的に分析する楽しさを伝えたいという気持ちと、共著『スマートモビリティ時代の地域とクルマ』を手にとってくれる方が一人でも増えるといいなという邪な気持ちで書いております。

地利値とは

アクセシビリティは、電車などのモビリティの発達や、山や川などの自然環境に左右されますが、今回は汎用的な議論を可能にするため、シンプルに地域と地域の隣接関係のみに着目します。

例えば、下図のような３つの隣り合うまちがあるときを考えます。

「この３つのまちから住む場所を選んでください」と命令された場合、真ん中のＢ市がなんとなく「地の利」がある気がしませんか？

この「なんとなく地の利あるが気がする感覚」を定量化するために「地利値」という概念を用います。詳細は省きますが、下図のような基礎的なグラフ理論で算出できます。

例で示した３つの隣り合うまちの場合、B市の地利値が「1.0」で最も高く、地の利のある場所であることが分かります。

参考として、他の単純な例も示します。

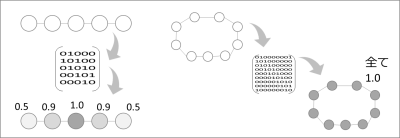
このように、あるまち（＝交通の結節点）を頂点、まちをつなぐ道を辺としたグラフの隣接行列の最大固有値に属する固有ベクトルを地利値といいます。今回は難しいことは考えずに、いろいろな地域の地利値を算出して遊んでみましょう。

それでは実際の地域に地利値を当てはめてみます。例えば、私の卒業した大学がある茨城県の市町村で考えると、地利値の高い市はどこになるでしょうか？県庁所在地の水戸市でしょうか？

上図のように茨城県で地利値がもっとも高い市はつくば市となりました。

つくば市は2023年の調査では人口増加率が全国トップの2.30%という数字でした¹。東京へのアクセスが良いつくばエクスプレスの駅周辺に子育て世帯が継続的に転入していることが理由のひとつだと思われます。

地利値を算出するのに鉄道網や経済指標などは加味していませんが、土地勘のある人にとってもある程度納得できる結果なのではないでしょうか？

他の地域でも地利値を見てみます。例えば私の地元、岩手県。

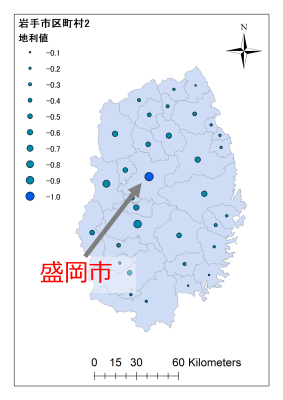
県庁所在地である盛岡市の地利値がもっとも大きくなります。盛岡市は県央に位置しており、周辺市町村からたくさんの人が働きにくる都市です。

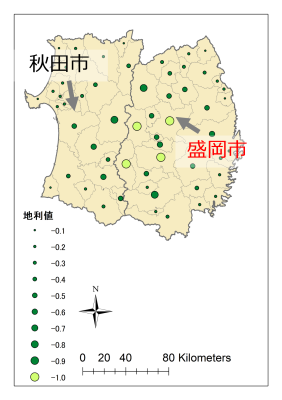
秋田県と並べてみても盛岡市の地利値が一番大きいです。西側が海に面している秋田市と比べて地の利があるのは盛岡市なのかもしれません。

九州に飛んで長崎県ではどうでしょう？

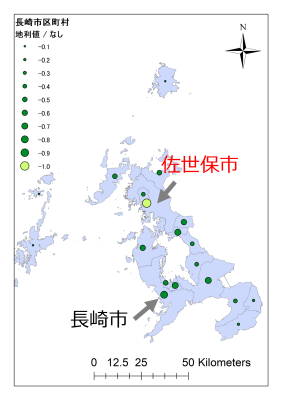
佐世保市です。Googleで検索すると、県庁所在地である長崎市との対決をあおる記事²が複数出てきますので、佐世保市が長崎市に並んで住みやすい市であるという感覚があるようです。

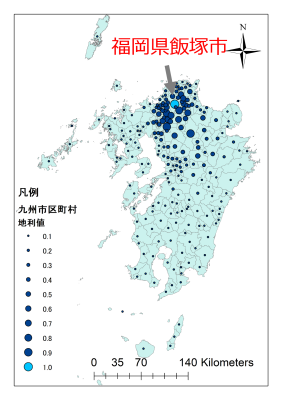
九州地方で地利値がもっとも高い場所は福岡県飯塚市です。これだけだと少し感覚と外れるかもしれませんが、九州全体でみると地利値が高い地域は福岡県に集中しており、政令指定都市2市が位置する福岡県の地の利が読み取れます。

最後に、全国の市町村で比べてみた時、最も地利値が大きい場所はどこでしょうか？

ぐちゃっとしていて分かりづらいですが、長野県松本市です。松本市と言えば、松本城がありますが、日本で最も地の利がある市と言われてもピンと来ないかもしれません。

気になる方は松本市の地利値が最も高くなる理由を考えてみてください（投げっぱなし）。

本記事では、土地勘に頼らずに地の利がある場所をみつけられる「地利値」という概念を紹介しました。

グラフの中心性を図る尺度は他にも様々ありますし³、グラフ理論に限らない他のアプローチでも定量的に「地の利」がある場所を探すことが出来るかもしれません。

地図は眺めたり、分析したりすることで、いつも新しい発見を得られます。本記事を読んで興味を持った方はぜひ探求してみてください。

共著『スマートモビリティ時代の地域とクルマ』では、（地利値は出てきませんが）都市と地域の課題を数理的アプローチで分析/解決しています。秋の読書候補におすすめです。

また、本記事冒頭のイラストはBingのImage Creatorによって生成したものです。