
こんにちは。ペンギンになりたいエンジニアの島ノ江です。
普段はCSIGというサイバーセキュリティのグループに所属していて、「FutureVuls」という脆弱性管理サービスの開発・営業などを行なっています。
秋のブログ週間の連載の17本目、「学習のSHA」というタイトルです。
暗号技術について学んでいると「ハッシュ値」という言葉に出会いますが、あまり詳細を追ったことはありませんでした。そこで今回はハッシュ関数およびその代表としてSHAに関する歴史や種類についてまとめます。念のため注意しますが、本記事と某アニメとは何も関係ありません。本当に。
本記事は次の2つを一次情報として参照しています。
せっかくなので、巻末に読書感想文として簡単に書籍の紹介もします。
寄稿の背景
本記事を書こうと思ったのは、ふと暗号技術の安全性に思いを馳せたことからでした。
11月2日(木)に斉藤さんが「初心者が暗号の基礎と歴史を勉強して見た」というタイトルで寄稿されています。これはシーザー暗号などのいわゆる古典暗号から公開鍵暗号などへの歴史を辿っている記事です。
このように暗号技術が変化してきたのには、技術などの発展に伴い暗号技術の安全性が変わっているからです。参考書籍にも「暗号は新しい安全な方式を提案する人と、それを解読しようとする人の両輪でよりよいものになっている」と書かれています。
では、「暗号技術のセキュリティ的な安全性とは?」という興味が湧くので、暗号技術の安全性に関する理解を深めよう、という流れでした。
ハッシュ関数とは
ハッシュ関数とは「文章や画像・動画などの任意のデータから、予め決められた範囲内の値を計算する関数」です。ハッシュ関数は決定的アルゴリズムで、同じ入力値に対して常に同じ値を返します。この入力値をメッセージ、出力のことをハッシュ値、ダイジェストなどとも言います。
ハッシュ関数は様々な場面で利用されていて、具体的には次のようなものがあります。
- 連想配列(JavaでのHashMapなど)
- データベース検索(ハッシュインデックスによる完全一致検索など)
- デジタル署名(送信者の認証など)
- ブロックチェーン技術(データの整合性の確認など)
このハッシュ関数の中で代表的なのが、本稿のタイトルにある「SHA」(Secure Hash Algorithm)です。これはNISTにより標準化されているハッシュアルゴリズムで、現代で広く用いられています。「エス・エイチ・エー」「シャー」と読まれていて、私は読みやすさから特にSHA256などは「シャー・ニゴロ」と読んでいます。
ハッシュ関数は現代で広く利用されている技術ですが、本記事では特に「暗号学的ハッシュ関数」について述べます。
暗号学的ハッシュ関数とは、さらに以下のような性質を持つハッシュ関数を指します。
出力サイズが一定
入力が1バイトであろうとGBであろうと、出力されるサイズは全く同じになる性質があります。
入力データのサイズによらずハッシュ値のサイズが同じだと、処理の効率性や互換性が向上します。
また、ハッシュ値のサイズが同じでないと、出力値から入力値の情報が得られてしまい、暗号分析にも悪用されかねません。

一方向性(原像計算困難性)
入力値からハッシュ値を求めることは簡単だが、その逆が難しい、という性質です。
ハッシュ値は分かるが元のメッセージが分からないという性質から、パスワードを比較的安全に保護することなどに利用されています。

衝突困難性
異なる2個の入力値から同じハッシュ値を得ること(衝突)が難しい(無視できる程度の確率である)、という性質です。
この性質を利用して、データを送る際にその入力値から計算したハッシュ値を併せて送ることで、データが改竄されていないかを確認できます。
これは、入力データが1ビットでも異なると、全く異なるハッシュ値が出力されるためです。

また、衝突困難性には「第二原像計算困難性」という性質があります。
これは、あるハッシュ値が与えられた時に、それと同じハッシュ値になる別のデータを見つけるのが難しい、という性質です。
小噺
その具体例として、学生時代の確率論の授業で、こんな確率を計算したことはあるでしょうか。
(1) N人が所属するクラスの中で、自分と同じ誕生日の人がいる確率
は?
(2) N人が所属するクラスの中で、誕生日が同じペアが存在する確率は?
(1)は自分と誕生日が同じ人を探すので第二原像を求める例、(2)はクラスの異なる2人で誕生日が一致するかを探すので衝突を見つける例になります。
計算自体は比較的単純なので、秋の夜長に学生時代に思いを馳せてやってみましょう。
です。wikipediaにちょうどいいグラフがあったので示します。
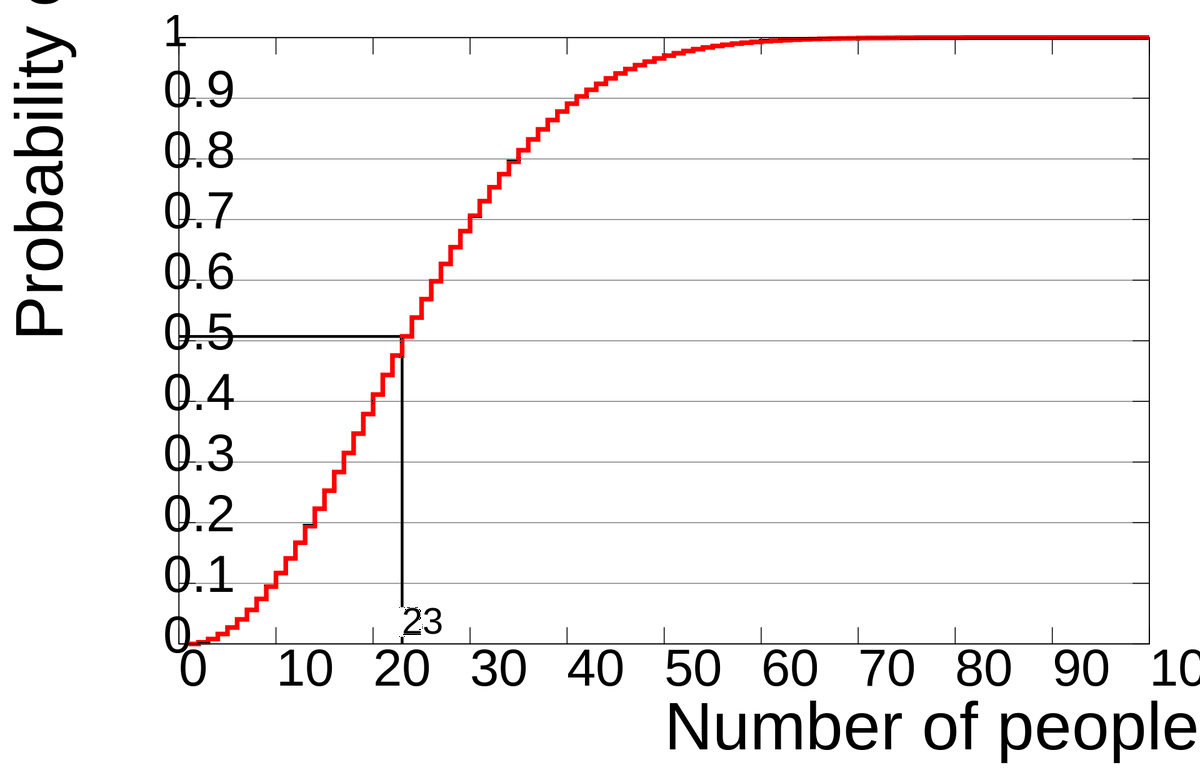
おおよそ
自分と同じ誕生日の人を探すと大変なのに、同じ誕生日になるペアが見つかるのはそれほど不思議ではない、というやや直感的でない結果が得られます(「誕生日のパラドックス」というそうです)。
このように、一般的には第二原像を見つけることより衝突を見つけることの方がずっと簡単です。
暗号技術の標準化を目指す組織とハッシュアルゴリズムの種類
このような暗号技術に関して、その安全性を監視・評価している機関が国内外にあります。
本資料で参考にしている NIST(National Institute of Standards and Technology:アメリカ国立標準技術研究所) は、ITL(Information Technology Laboratory:情報技術研究所) という研究部門で、このセキュリティに関する標準化をおこなっています。
日本では、CRYPTREC(CRYPTography Research and Evaluation Committees:暗号技術評価委員会) という機関が、国内の電子政府推奨暗号の安全性を評価・監視しています。
NISTは標準のハッシュ関数として、 FIPS 180-4 と FIPS 202 を公開しています。日本国内でも、電子政府推奨暗号リストとしてこれらの利用を公開しています。
FIPS 180-4では、以下の7つが推奨されるハッシュ関数として規定されました。なお、2011年にはSHA-1の使用を非推奨にする発表を出し、2022年12月にはSHA-1を廃止する発表が出ています(参考)
- SHA-1
- SHA-2(SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, SHA-512/256)
SHAの後ろについている数字がハッシュ関数の出力ビット数です。SHA-256は長さが256ビットのハッシュ値を返す、という形です。これらは要求されるセキュリティレベルによって使い分けられます。
FIPS-202では、SHA-2に加えてSHA-3が追加されました。SHAKEはSHA3を拡張したハッシュ関数で、出力のハッシュ値をセキュリティレベルに応じて変更できます。
- 固定長を返すハッシュ関数: SHA3-224, SHA3-256, SHA3-384, SHA3-512
- 可変長を返すハッシュ関数: SHAKE128, SHAKE256
ハッシュ関数の歴史
ここでは主なハッシュ関数の歴史に触れます。画像は参考図書にも掲載されているものです(引用元)
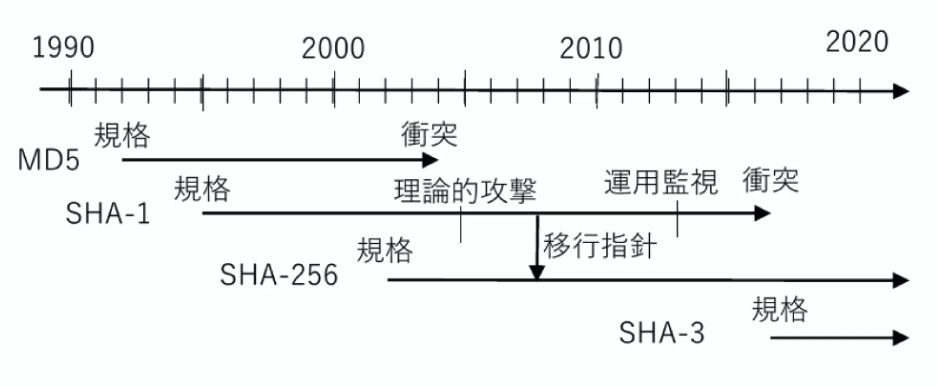
- 1992年にMD5が登場しましたが、暗号学的ハッシュ関数ではなかったこともあり、12年後に衝突困難性が破られてしまいました。メッセージから固定値(128bit)のハッシュ値を生成します。この関数は高速で単純だったことから、メッセージの整合性確認などで広く用いられたようです。
- SHA-1は1995年に標準化され、理論的な攻撃可能性の提案に10年かかり、2017年には衝突困難性が破られました。先述の通り、2011年にはSHA-1の使用を非推奨にする発表を出し、2022年12月にはSHA-1を廃止する流れになっています。
- SHA-2は2001年に標準化され、その中のSHA-256は現在も推奨暗号として広く利用されています。
- SHA-3は、SHA-1の攻撃突破が危惧された頃に、これまでとは異なる構造のアルゴリズムが必要になるだろうという危惧から考えられたハッシュ関数群です。しかし幸いなことにSHA-2の衝突困難性がなかなか破られておらず、あまり積極的には利用されていません。
SHA-2, SHA-3の理論的な側面まで深掘りをしたかったのですが、それを書くには余白が足りず 細かくて時間が足りないので、ここでは割愛します。気になる方は、参考書籍やNISTのFIPSの資料、および参考書籍の巻末に掲載されている資料を参照してください。
暗号技術の安全性とは
暗号技術をせっかく使うなら、理想的には「どうやっても絶対に破られない暗号」を使いたいです。しかし、小さな秘密鍵を使って大きな平文を暗号化しようとする以上、理論的にこのような理想の暗号技術を作ることはできません。そこで、「理想の安全性はないけれども現実的には破れないだろう」という暗号を考え、それを測る指標として「セキュリティパラメータ」というもので計算コストを考えます。
例えば、共通鍵暗号では鍵長が N ビットであればその種類は
ハッシュ関数では、衝突困難性を破るのに必要なコストはおおよそ
SHA-512の方が安全なのに、なぜSHA-256の方が広く利用されているのか? という点については、次のような背景があるようです。
- SHA-512の方がより安全ではあるが、SHA-256でも現時点では十分なセキュリティレベルがあり、かつその方がリソース使用量が小さくて済むため
- 広く利用されており、他のシステムやプロトコルとの互換性があるため
- 暗号技術が広く利用されているのはそれだけ検証が多くなされていることでもあり、信頼感があるため
なお参考書籍によると、SHA-256およびSHA-512での内部構造を追っていくと、64ビットCPUで大きなデータを扱う場合には内部処理過程の関係でSHA-256よりSHA-512の方が高速に計算できるようです。これは知らなかったので、内部構造を知って驚きました。
なお、このような安全性というのはあくまで「現在の技術・攻撃手法の範囲で」安全というものであり、未来永劫安全というわけではありません。例えば、昨今発展している量子計算機を用いるとSHA-2の攻撃可能性が進展している研究もあります。また、よりよい攻撃手法が発見されて、セキュリティパラメータが下がる可能性もあります。ある日突然攻撃手法が発展し、人類は思い出した…ということになる可能性もあるので、注意は必要です。
まとめ
本稿では暗号学的ハッシュ関数について整理し、その種類および歴史を追いました。自分はSHA-256には馴染みがありましたが、SHA3についてはあまり知らず、本稿を書く際に色々と学ぶことができて良い機会となりました。
あまり実装的な内容は書かないとのことなので、今回はコードについても記載していません。例えばGo言語では、SHA-256などは crypto パッケージに含まれているので、ご参照ください。
詳細を書ききれていないところも多くあるため、引用資料先のページなども参考にしていただけると幸いです。それでは快適なハッシュライフ(?)をお送りください。
終わりに書籍の紹介
本書は広く「暗号と認証」をテーマに解説している参考書です。全部で9章で構成されており、各章がいくつかのセクションごとに分かれていてまとめもあるため、テンポ良く読み進めることができます。
第3章から「共通鍵暗号」「公開鍵暗号」「認証」の解説があり、最終章には「高機能な暗号技術」と題してゼロ知識証明や量子コンピュータなどの解説がされます。
個人的に思う本書の大きな特徴は、数式の解説も交えて暗号技術を解説するという点にあると思います。離散対数問題や楕円曲線暗号といった、高度な暗号技術を学ぶために必要な概念の基本も説明されています。暗号技術を学ぶにはどうしても高度な数学が絡みますが、本書はその部分をなるべく平易に解説していて、暗号技術を学習するハードルを下げている点が高評価です。
ただし、その分読み手を選んでしまう本かなという印象です。理系出身の方や、基本情報技術者試験などを経てより詳細に暗号技術について知りたい、という意欲のある方には良いかもしれません。巻末も充実しているので、本書を起点にさらに深く学習していくのに役立つ本だと思います。
本記事はこれで終わります。最後まで読んでいただきありがとうございました。
アイキャッチ画像はBing Image Creatorを利用しました。