はじめに

こんにちは、はじめまして、流通グループの市川です。

春の入門連載20日目となる、今回のテーマはベイズ推定です。選定の理由はこうです。

業務で直接利用しているわけではないのですが、データ分析にはもともと興味があり、普段から社内の数人の有志メンバーを集めてチームを組んでデータ分析コンペなどにちまちまと参加していました。

しかし、ベイズ推定というものは名前くらいは聞いたことがあるものの今まで触れてきていませんでした。今回、せっかくの春の入門連載という機会に Stanによるベイズ推定 に初挑戦します。

また、分析対象も、個人的に興味のあった株価推移の予測にしてみることにしました。

この記事では、簡易的なベイズモデルを構築して、株価推移というある種の予測問題を解くまでの流れをベイズ初心者目線でご紹介します。

なお、当然ですが投資取引への勧誘等を目的にしたものではなく、本情報を利用した際の取引等は全て自己の責任において行ってください。

目次

1. ベイズ推定とは
2. Stanとは
3. Stanのインストール
4. 株価データの取得と前処理
5. ベイズモデルの構築とStanでの実装
6. 株価予測の実施と評価
7. 最後に
8. 参考文献
9. 補足

ベイズ推定とは

ベイズ推定とは、ベイズの定理を使った統計的推定の一種です。特徴として、「不確実性を定量化するときに、確率を明示的に使うこと」があります。

こう聞くとあまりピンとこないかもしれませんが、例を出すと、明日の株価は上がるのか下がるのかよくわからない、というときでも「よくわからない」としてしまうのではなく「明日の株価が上がる確率は40％くらいかな」と確率を使って評価を試みます。

詳細は補足にまとめているので興味のある方はみてみてください。

Stanとは

Stanが何か簡単に紹介します。StanはC++で書かれた統計的推論のための確率的プログラミング言語で、ベイズ推定を高速で処理できるのが特徴です。

ベイズ推定を行う際に、厳密に推定するためには非常に複雑な計算を行わなければならないケースが頻繁に発生します。しかし、Stanを利用することで、複雑な計算を回避して近似的に推定を行うMCMCと呼ばれる手法を簡単に実装できます

Stanは、RやPythonといったデータ分析言語から利用できます。

今回はPythonからStanを用いるためのパッケージPyStanを使っていきます。

Stanのインストール

PyStanのインストール方法の詳細はこちらを参照してください。

https://pystan.readthedocs.io/en/latest/

pipでインストール可能です。

pip install pystan

PythonとPyStanの関係ですが、今回はデータの読み込みや可視化といった基本的なデータ処理をPythonで行い、StanはMCMCの実行のみで利用します。

株価データの取得と前処理

今回はYahoo Financeから過去5年分の日経平均株価のデータを取得して学習と予測に利用します。

まず、必要なパッケージとデータを読み込みます。

import yfinance as yf
import stan
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 日経平均のティッカーシンボル"^N225"
ticker_symbol = "^N225"

# yfinanceのdownloadメソッドで過去5年分の日次データを取得
df = yf.download(ticker_symbol, period="5y")

データの中身を確認してみます。

print(df.describe())
print(df.shape)

               Open          High           Low         Close     Adj Close        Volume
count   1219.000000   1219.000000   1219.000000   1219.000000   1219.000000  1.219000e+03
mean   24987.351836  25114.861626  24846.183244  24986.802835  24986.802835  7.191682e+07
std     3220.081547   3227.214291   3215.333714   3219.545197   3219.545197  2.091914e+07
min    16570.570312  17049.029297  16358.190430  16552.830078  16552.830078  0.000000e+00
25%    22186.509766  22307.625000  22065.250000  22201.190430  22201.190430  5.940000e+07
50%    25405.640625  25555.369141  25215.310547  25349.599609  25349.599609  6.930000e+07
75%    27886.849609  28036.350586  27706.930664  27893.959961  27893.959961  8.050000e+07
max    30847.359375  30924.570312  30679.160156  30808.349609  30808.349609  2.334000e+08
(1219, 6)

データには、以下の株価情報が日別で1219日分含まれているようです。

• Date : 日付(インデックス)
• Open : 始値
• High : 高値
• Low : 安値
• Close : 終値
• Adj Close : 調整後終値
• Volume : 出来高

このうち、終値のデータを予測対象の株価情報として利用します。

続いてデータの前処理として、カラムを追加していきます。

今回は株価のテクニカル分析のようなイメージで予測を行ってみたいので、2種類の移動平均を計算して追加することとします。

• ma_5 : 5日移動平均
• ma_25 : 25日移動平均

# 5日、25日移動平均を計算
df['ma_5'] = df['Close'].rolling(window=5).mean()
df['ma_25'] = df['Close'].rolling(window=25).mean()

# 25日移動平均が計算できない最初の25日間を除外
df = df.iloc[25:]

ついでに、移動平均が計算できない最初の25日間を除外します。

さて、ここまででデータの前処理は完了です。

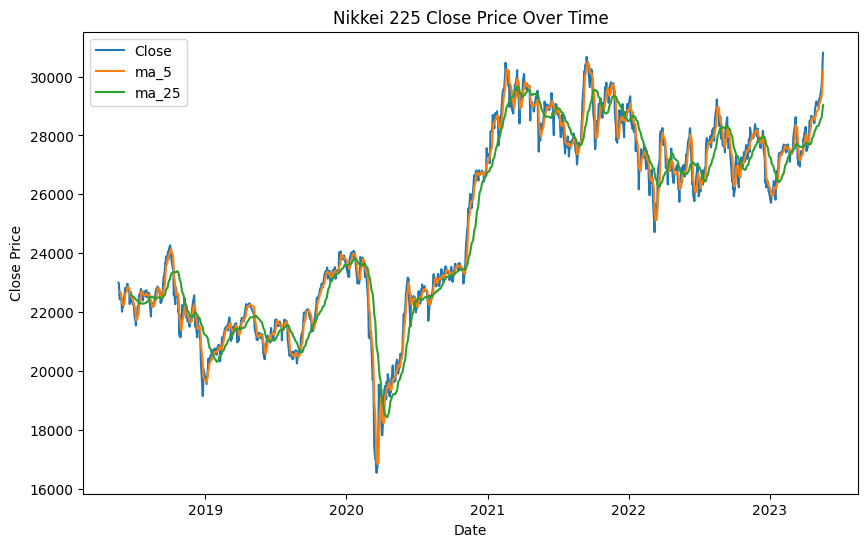
一度データを可視化しておきます。

予測のためにはモデル設計を行うことが必要ですが、その際に実際のデータの分布を理解しておくことが望ましいです。

今回、特に複雑なモデルは設定しませんが、流れとしてデータの可視化は習慣づけておくとよいのかなと思います。

# データの可視化
plt.figure(figsize=(10,6))
plt.plot(df.index, df["Close"], label="Close")
plt.plot(df.index, df["ma_5"], label="ma_5")
plt.plot(df.index, df["ma_25"], label="ma_25")
plt.xlabel("Date")
plt.ylabel("Close Price")
plt.title("Nikkei 225 Close Price Over Time")
plt.legend()
plt.show()

ベイズモデルの構築とStanでの実装

では、ここからモデル構築とStanでの実装に入っていきます。予測までの流れは以下のとおりです。

1. モデルの設計
2. Stanファイルの実装
3. MCMC実行
4. 事後分布の可視化
5. 予測の検証

このパートでは、Stanファイルの実装までを行います。

モデルの設計

まず、ベイズモデルを設計します。

今回は複雑なモデルは使わず、前日の終値、移動平均から当日の終値を予測するため、シンプルな線形回帰モデルを使用します。

以下にモデルの構造を示します。

前日の株価、移動平均にそれぞれ係数をかけて調整した上で、前日の株価や移動平均すべて0だった場合の当日の株価を表す切片を加算することで、当日の株価を予測します。

Stanファイルの実装

では、Stanファイルを実装していきます。

stanコードは、基本的にdataブロック、parametersブロック、modelブロックの3つのブロックが必要です。

• dataブロック: 使用するデータやサンプルサイズなどの情報を指定します
• parametersブロック: 後分布を得たいパラメータの一覧を定義します
• modelブロック:事前分布や尤度を指定します。事前分布を指定しない場合、 の一様分布が標準の無情報事前分布として用いられます

今回はさらに、テストデータに基づいて予測値を生成するためのgenerated quantitiesブロックを追加しています。

dataブロック

まずは、dataブロックから見ていきます。

data {
    int<lower=0> N;         // 訓練データのサンプルサイズ
    vector[N] Close;        // 訓練データの終値
    vector[N] MA5;          // 訓練データの5日移動平均
    vector[N] MA25;         // 訓練データの25日移動平均

    int<lower=0> N_test;        // テストデータのサンプルサイズ
    vector[N_test] Close_test;  // テストデータの終値
    vector[N_test] MA5_test;    // テストデータの5日移動平均
    vector[N_test] MA25_test;   // テストデータの25日移動平均
}

dataブロックにはサンプルサイズとデータを指定しています。

また、訓練用、テスト用に別々のデータを指定していますが、この後データを定義する際に分割して渡してあげます。

parametersブロック

parameters {
    real alpha;             // 切片
    real beta1;             // 前日終値の係数
    real beta2;             // 5日移動平均の係数
    real beta3;             // 25日移動平均の係数
    real<lower=0> sigma;    // 標準偏差
}

parametersブロックでは、推定すべきパラメータを指定します。今回は線形回帰モデルを想定するため、切片alphaと各項目の係数beta1~3、データのばらつきとして標準偏差sigmaを定義しています。

modelブロック

model {
    for (n in 2:N) {
        Close[n] ~ normal(alpha + beta1*Close[n-1] + beta2*MA5[n-1] + beta3*MA25[n-1], sigma);
    }
}

modelブロックでは、観測された終値（Close[n]）が、前日の終値（Close[n-1]）、5日移動平均（MA5[n-1]）、25日移動平均（MA25[n-1]）とそれらの対応する係数（beta1、beta2、beta3）、そして切片（alpha）によって定義される正規分布からサンプリングされたと仮定しています。

generated quantitiesブロック

generated quantities {
    vector[N_test] Close_prediction;
    for (n in 2:N_test) {
        Close_prediction[n] = normal_rng(alpha + beta1*Close_test[n-1] + beta2*MA5_test[n-1] + beta3*MA25_test[n-1], sigma);
    }
}

generated quantitiesブロックは、終値の予測値（Close_prediction）を生成するパートです。

テストデータの各要素（前日の終値、5日移動平均、25日移動平均）に対応するパラメータ（alpha、beta1、beta2、beta3）を用いて予測値を算出し、その予測値が正規分布に従うと仮定してサンプリングを行います。

続いて、stanに渡すデータを定義します。

ここで、訓練データとテストデータを分割して辞書にデータを格納しています。

# 訓練データとテストデータに分割（訓練データ:テストデータ = 8:2）
train, test = train_test_split(df, test_size=0.2, shuffle=False)

# データを辞書に格納
data_dict = {
    'N': len(train),
    'Close': train['Close'].values,
    'MA5': train['ma_5'].values,
    'MA25': train['ma_25'].values,
    'N_test': len(test),
    'Close_test': test['Close'].values,
    'MA5_test': test['ma_5'].values,
    'MA25_test': test['ma_25'].values
}

株価予測の実施と評価

Stanファイルの実装ができました。
ここから予測の実施と評価に入っていきます。

MCMC実行

MCMCを実行します。Stanモデルをビルドし、サンプリングを行っていきます。

# stanモデルをビルド
posterior = stan.build(stan_model, data=data_dict, random_seed=1)

# サンプリング
fit = posterior.sample(num_chains=4, num_samples=1000)

stanモデルのビルドではrandom_seedを指定しています。

これは生成される乱数値の固定のために使用します。分析の再現性のため毎回設定しておくことが望ましいです。

また、サンプリングで設定しているnum_chainsはチェーン数でMCMCによる1セットの乱数生成を行う回数のこと、num_samplesは乱数生成の繰り返し回数、すなわち1セットごとに生成される乱数の個数です。

今回は1000回の乱数生成を4セット行い、4000個のサンプリングを行うという設定をしていることになります。(実際には、デフォルトで間引き数であるthin=2が設定されているため、2つの乱数生成に付き1つが採用されます。そのため、ログ上では8000個の乱数生成が行われているような表示が出るかと思います。)

結果が出るまで数分程度かかるかもしれません。

事後分布の可視化

サンプリングが完了すると結果がFitクラスで得られます。

ここから、事後分布の可視化をしてみます。

# MCMCサンプリング結果からパラメータのサンプリング結果を取得
alpha_samples = fit['alpha'][0]
beta1_samples = fit['beta1'][0]
beta2_samples = fit['beta2'][0]
beta3_samples = fit['beta3'][0]
sigma_samples = fit['sigma'][0]

# 各パラメータのサンプル
param_names = ['alpha', 'beta1', 'beta2', 'beta3', 'sigma']
samples = {
    'alpha': alpha_samples,
    'beta1': beta1_samples,
    'beta2': beta2_samples,
    'beta3': beta3_samples,
    'sigma': sigma_samples
}

# パラメータ毎にプロット
for param_name in param_names:
    fig, axes = plt.subplots(1, 2, figsize=(10, 5))
    param_samples = samples[param_name]

    # 事後分布
    sns.histplot(param_samples, kde=True, ax=axes[0], color='gray')
    axes[0].set_title(f'Posterior distribution of {param_name}_samples')

    # トレースプロット
    for i in range(4):
        axes[1].plot(param_samples[i*1000:(i+1)*1000], color=colors[i], alpha=.5, label=f'Chain {i+1}')

    axes[1].set_ylabel('Value')
    axes[1].set_title(f'Trace plot of {param_name}_samples')
    axes[1].legend(loc='upper right')
    plt.tight_layout()
    plt.show()

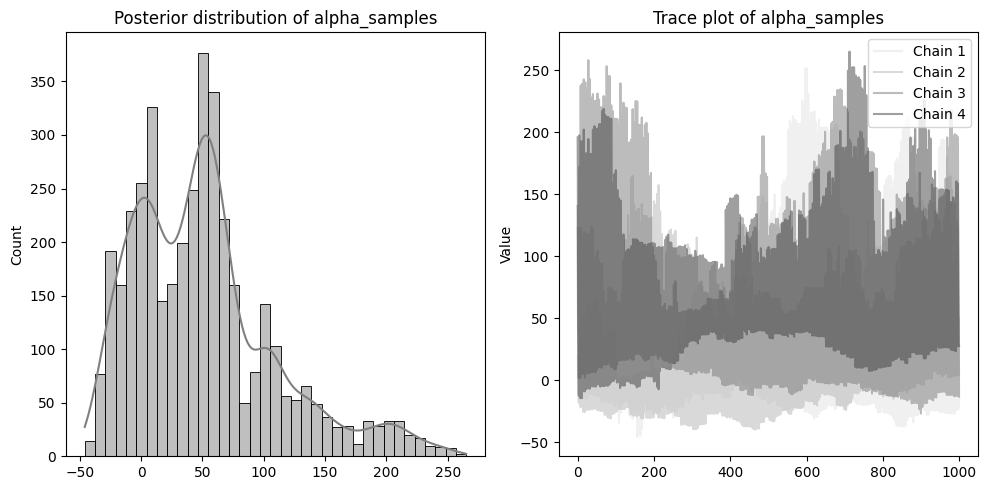
左側に分布を、右側に収束の確認のためのトレースプロットを配置しています。

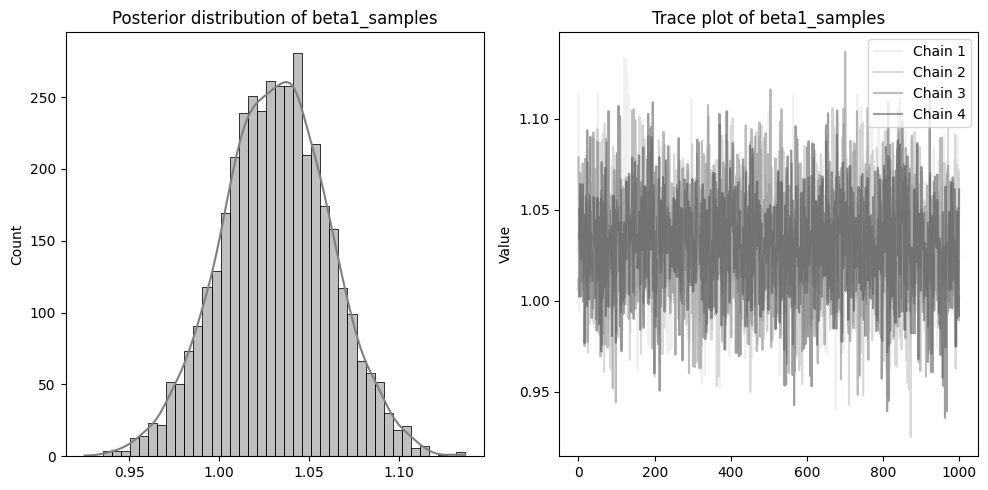
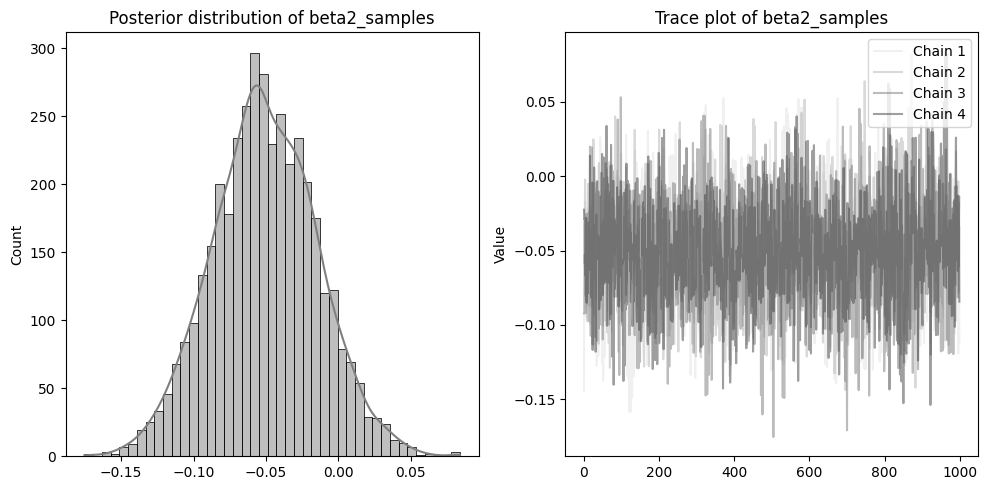
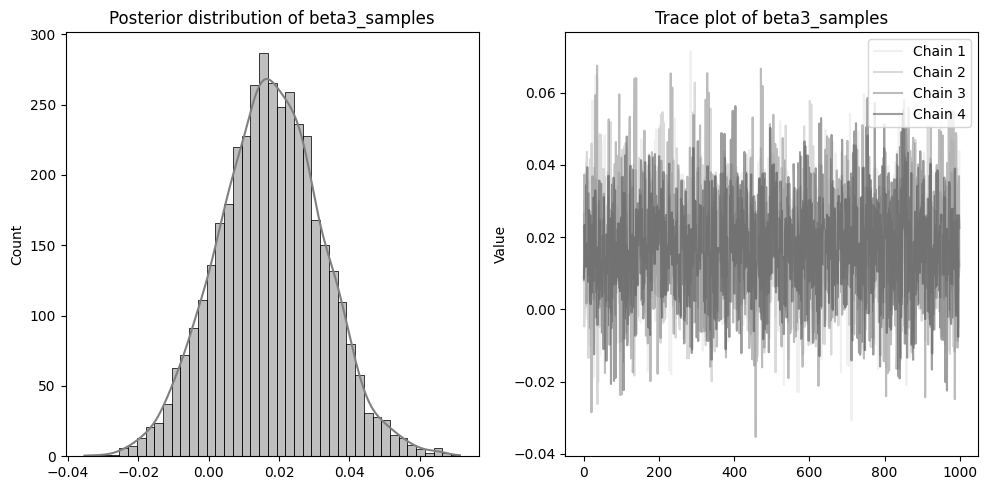
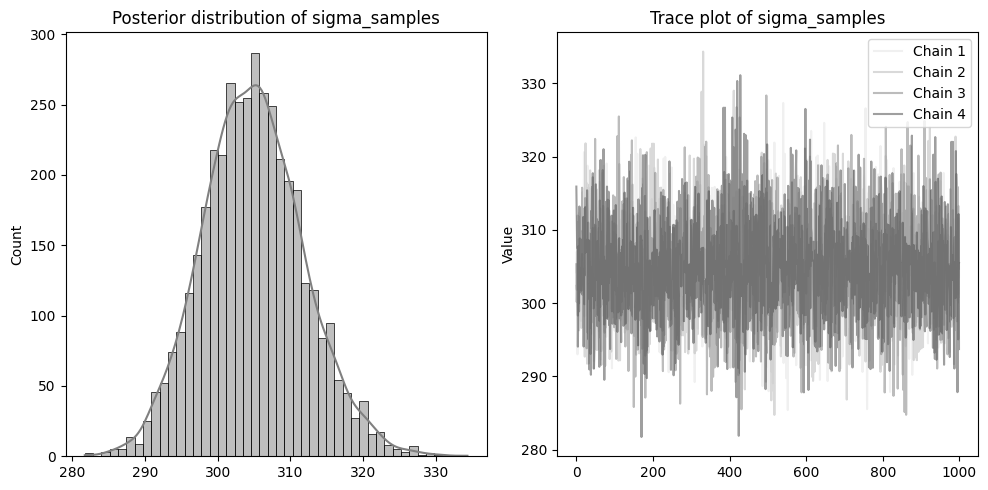
beta1~3やsigmaのトレースプロットのように、4本のチェーンが混ざりあった状態であれば収束できています。

逆にalphaのような状態は、うまく収束していないです。収束しない場合、予測結果の信頼性が低くなる可能性があるため注意が必要です。

収束の改善のためには、サンプリング方法を見直す、サンプルサイズを増やす、モデル自体の改良などが挙げられます。今回alphaが収束しなかったのは、株価の推移のような複雑な現象を、非常に単純な線形回帰モデルとして仮定したことが原因になっているかもしれません。

本来であればここでパラメータが収束するようチューニングを行うことになるかと思いますが、今回は流れの理解を目指しているのでこのまま予測の検証に進みます。

予測の検証

予測値は、Close_predictionとしてサンプリングされているので、このデータを実際の終値と比較してみましょう。

Close_predictionでは各時点に対して4000個の推定値がサンプリングされています。

このままでは比較も可視化も難しいので95％信頼区間を算出してプロットしてみます。95％信頼区間は、データのうち大きすぎる2.5％と小さすぎる2.5％を除いた95％のデータが含まれる区間と考えてください。

# テストデータの実際の終値
actual_close = test['Close'].values

# サンプリングされた終値の推定値
predicted_close = fit['Close_prediction']

# 95%信頼区間の設定
lower_bound = np.percentile(predicted_close, 2.5, axis=1)
upper_bound = np.percentile(predicted_close, 97.5, axis=1)

# グラフのプロット
plt.figure(figsize=(10, 6))
plt.plot(test.index, actual_close, label='Actual Close Price')
plt.fill_between(test.index, lower_bound, upper_bound, alpha=0.3, label='95% CI')
plt.xlabel('Date')
plt.ylabel('Close Price')
plt.title('Comparison of Actual and Predicted Close Prices with 95% CI')
plt.legend()
plt.show()

結果:

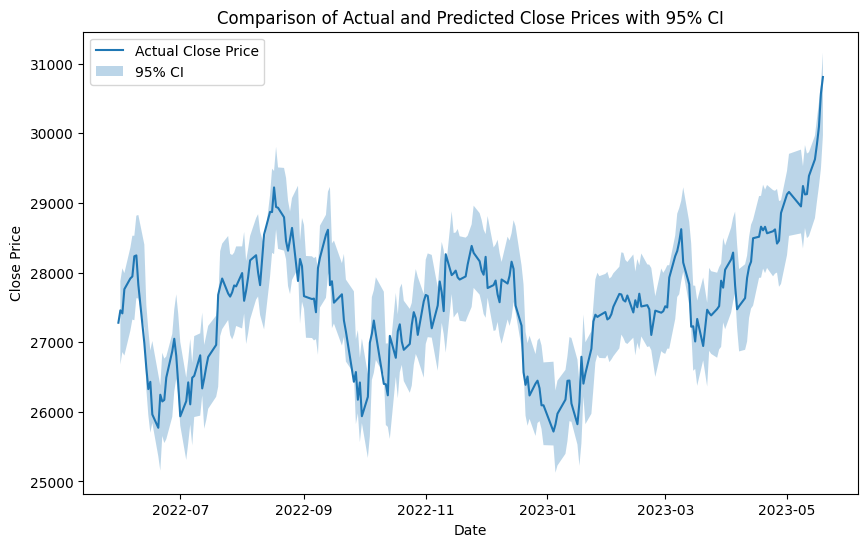
実線が実際に観測された株価を、薄い青のエリアが今回のモデルで推定された株価の範囲となります。

こうしてみるとかなりよい精度で予測されているように見えます。

少なくとも実際に観測された株価が95％信頼区間に含まれていない箇所はほとんどなさそうです。

しかし、信頼区間のような幅のある予測のままでは、具体的な判断(買いなのか売りなのか)はなかなか難しいです。

そのため、サンプリングされた株価の推定値の平均を計算し、その値が前日の株価に対して、上がっているのか、それとも下がっているのかを判定してみます。

そして、この上がるか下がるかの予測がどの程度の精度であるかを確かめてみましょう。

# 予測値が上がるか下がるか（上がる: 1, 下がる: 0）
pred_direction = (predicted_close[1:, :].mean(axis=1) > actual_close[:-1]).astype(int)

# 実際の値が上がるか下がるか（上がる: 1, 下がる: 0）
actual_direction = (actual_close[1:] > actual_close[:-1]).astype(int)

# 予測結果と実際の結果の一致率
accuracy = np.mean(pred_direction == actual_direction)

# 結果
print('Accuracy: ', accuracy)

結果:

Accuracy:  0.5126050420168067

正解率は約51.3％という結果でした。

完全ランダムだと50％になるはずなのでそれよりはほんの少しプラスですね。

このちょいプラスだという結果が有意なものかの検証まではできていないため、誤差の範囲とも言えそうですがひとまず株価推移予測を行うという当初の目的はクリアしたと言ってよいでしょう。

最後に

ベイズ推定を用いて株価予測ができました。

全く使ったことがない状態から、簡単なモデルであれば推定までできるところまで行けたので、今後、データ分析コンペなどで活用して分析のオプションの1つとしてベイズを使いこなせるようにしていきたいです。

また、Stanの扱い方も、設計したモデルをコードに落とすことができればそれほど苦労せず動かせることがわかったのは収穫でした。正直、ベイズ推定に対しては食わず嫌い的な状態だったので良い機会になりました。

今回扱えなかったより複雑なベイズモデルとしては、時系列モデルとして知られる状態空間モデルや隠れマルコフモデルといったものもあります。これらのモデルでは、株価の時間依存性や潜在的な状態を考慮できるので、これらを仮定することでより精度の高い予測が可能になるかもしれません。

興味のある方はぜひチャレンジしてみると面白いと思います。

次は小橋さんのTechnology_Radar_の機械学習関連技術を見てみるです。

参考文献

https://www.kspub.co.jp/book/detail/5165362.html

補足

以下では、ベイズの定理やMCMCについてまとめています。

まず、ベイズの定理です。公式としては以下のようになります。

ベイズの定理では、しばしば「事前確率を事後確率に更新する」という言い方がなされます。

事前確率とは、「データが得られる前に想定された確率」のことで、事後確率とは、「データが得られたあとに想定する確率」です。上の式で、事前確率 は、尤度 と周辺尤度 の比を使って事後確率である を更新しています。

さらっと流してしまいましたが、尤度は「ある仮定が与えられたという条件のもとで、データ得られる確率」、周辺尤度は「データが得られる平均的な確率」と解釈されます。

例を見てみましょう。

正しいコインと表が出やすいイカサマコインの2枚のコインがあります。そのうち1枚を手渡されました。手渡されたコインがイカサマコインなのかそうでないのかは「よくわからない」という状況です。この「イカサマかどうかよくわからない」という状況を、確率を使って定量的に評価することを試みます

コインが手渡された直後、これ以上何の情報もないときに考えた「渡されたコインがイカサマコインである確率」が事前確率です。
一方、コインを1回投げて、表という結果が出たとしましょう。「コインが表になったというデータ」が与えられた下での「渡されたコインがイカサマコインである確率」が事後確率となります。

事前確率をどのように指定するかですが、事前の情報がない場合、理由不十分の原則に基づき等しい確率を各々の仮定に割り当てます。
そのため、イカサマコインが渡されたという事前確率 は0.5、
正しいコインが渡されたという事前確率 は0.5となります

尤度は事前に計算できると仮定します。例えば、「イカサマコインは75%の確率で表が出る」また「正しいコインは50%の確率で表が出る」ということがわかっていたとします。

周辺尤度は「手持ちのデータが得られる平均的な確率となり、

これを計算すると、 となります。

コインを投げて表という結果がでたあとに想定する「渡されたコインがイカサマコインであると想定する確率」すなわち事後確率は、
事後確率:

このようにベイズの定理を用いて事前確率を事後確率に更新することで更新していくことをベイズ更新などと呼び、ベイズ推定でもこの考え方に基づきパラメータの推定、データの予測を行っていきます。

ただし、先の例のように推定値を1つだけ提示するのではなく、確率分布で定量化することを試みます。

そこで、ベイズの定理を確率分布に拡張した以下の式を用います。

は事前確率を、 が事前確率分布を表します。
はデータの尤度を は尤度関数を意味し、 は周辺尤度となります。

この周辺尤度は正規化定数となり、この積分計算が非常に複雑で困難なことがしばしば発生します。

例えば、事後分布の確率密度関数 が得られているときに「連続型の確率分布に従うパラメータ が から の間に入る確率」を求めるために、以下の積分計算が必要になります。

そこで、事後分布が複雑になりすぎて積分ができないという問題をどうにか解決するための手段にMCMCがあります。

MCMCはマルコフ連鎖モンテカルロ法の略で、マルコフ連鎖を利用して乱数を生成する手法です。
では、なぜただの乱数生成から事後分布がわかることになるのでしょうか。

ここで、一旦マルコフ連鎖とはなにかを紹介します。

確率変数が時間の経過とともに変化していく数理モデルを確率過程と呼び、一般的な確率過程では以下のように全ての歴史をもとに確率分布が記述されます。

これに対して、現在の状態は1時点前の状態のみに依存し、それ以前の過去の状態には依存しないような確率分布は、

となります。このような確率過程をマルコフ連鎖と呼びます。

身近な例として、天気を考えてみます。

例えば、ある地域の天気が「晴れ」「曇り」「雨」の3状態のみを取るとします。そして、ある日の天気が前日の天気にのみ依存し、それ以前の天気には影響を受けないとします。
これがマルコフ連鎖の特性です。
具体的には、前日が晴れであれば次の日が晴れる確率が70%、曇りになる確率が20%、雨になる確率が10%、といった具体的な確率があると考えます。同様に、前日が曇りや雨であった場合の次の日の天気に対する確率も設定します。このような1時点前の状態が与えられたときの条件付き確率のことを「遷移核」と呼びます。
この天気の遷移を何日も続けていくと、ある一定の確率分布に収束していきます。
たとえば、365日間天気の遷移を観察したとします。その結果、全体として晴れの日が60%、曇りの日が30%、雨の日が10%という比率になったとします。このように一定の比率に収束した確率分布を「定常分布」と呼びます。
そして、マルコフ連鎖では、どの初期状態からスタートしても（つまり、1日目が晴れであろうと雨であろうと）、長期的にはこの定常分布に収束するという性質があります。

MCMCでは、このマルコフ連鎖の性質を利用して、求めたい確率分布をサンプリングします。
天気の例では、「晴れの日が60％、曇りの日が30％、雨の日が10％」という分布が求めたい確率分布(=事後確率分布)になります。

つまり、遷移核がわかっていれば、マルコフ連鎖を活用して乱数を生成でき、マルコフ連鎖が定常分布に収束するならば定常分布に従う乱数も得られそうです。

いまやりたかったことは、「事後分布を評価できないので、事後分布からたくさんサンプリングをして事後分布の評価を近似すること」でした。
もし、定常分布が事後分布のマルコフ連鎖を構成できれば、遷移核に従い現在の状態から次の状態へ分布を変えずに遷移できます。つまり、遷移核がうまく設定でき、定常分布を事後分布と見立てるとことができれば、今回の目的は達成できそうです。

次の問題は、「定常分布が事後分布になるマルコフ連鎖」をどうやって得るか。言い換えると遷移核をどのように設定すればよいかですが、これには様々な方法があり有名なものに[MH法]や[HMC法]があります。

今回はStanで採用されているHMC法を利用することになります。
(実際にはHMC法を発展させたNUTSというアルゴリズムが使われているようです。)