Future Tech Blog
フューチャー技術ブログ
Programmingカテゴリ

GoとSuffixArray

フューチャー夏休みの自由研究連載の5回目です。

はじめに

TIG の辻です。

Go は標準ライブラリが充実しているとよく言われます。標準ライブラリだけで、HTTP サーバを作れたり、暗号化処理や、JSON や CSV といったデータ形式を扱うことができます。go list std | grep -v vendor | wc -l としてパッケージ数を見てみると、約 200 ものパッケージが存在することがわかります。本記事では、その多くの Go の標準ライブラリの中でも、個人的に面白いなと思ったライブラリを紹介したいと思います。suffixarray パッケージです。

suffixarray パッケージは Suffix Array を扱うライブラリです。suffixarray パッケージの魅力を感じるには、まず Suffix Array とは何か？ を知る必要があるでしょう。

Suffix Arrayとは

Suffix Array はデータ構造の 1 つです。1990 年に Udi Manber, Gene Myers によって考案されました。Suffix Array を用いると、検索したい任意の文字列から、漏れなく高速に文字列を検索できます。全文検索やデータ圧縮といった応用があります。

Suffix Array は文字列のすべての suffix を辞書順でソートし、それぞれの suffix の元の文字列における開始位置を保持する配列です。長さが n である文字列 T の suffix とは 1 ≦ i ≦ n なる i について T の i 文字目から n 文字目までの部分文字列のことを指します。具体的に banana という文字列で考えてみます。banana のおける suffix は以下の 6 つです。

  • banana
  • anana
  • nana
  • ana
  • na
  • a

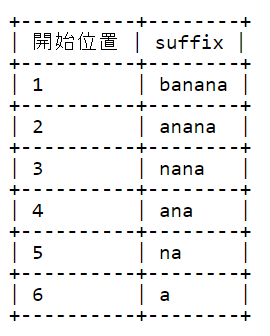
各 suffix の開始位置をあわせて記載すると以下のようになります。

開始位置 suffix
1 banana
2 anana
3 nana
4 ana
5 na
6 a

これらの suffix を辞書順でソートすると以下のようになります。

開始位置 suffix
6 a
4 ana
2 anana
1 banana
5 na
3 nana

よって、banana の文字列における Suffix Array とは [6, 4, 2, 1, 5, 3] という配列になります。suffix の開始位置があれば元の suffix を構成でき、開始位置から n 文字目までの部分文字列になります。banana における suffix の開始位置が 3 であれば元の suffix は 3 文字目から 6 文字目までの部分文字列であるため、nana という suffix であることがわかります。

文字列のパターンマッチング

Suffix Array がどのようなデータ構造であるか分かりました。次に Suffix Array を用いて、文字列をパターンマッチングすることを考えてみます。banana という文字列から an という文字列をパターンマッチングすることを考えてみます。banana ですから、赤文字である 2 文字目から 3 文字目の an と、青文字である 4 文字目から 5 文字目の an の 2 箇所でマッチします。文字列 T の任意の部分文字列は、その出現位置を開始位置とする T の suffix の prefix です。つまり an であれば suffix ana の prefix である an と suffix anana の prefix である an です。このように文字列 P を prefix としてもつような、T の suffix を探索することによって、文字列のパターンマッチングができます。Suffix Array は文字列の suffix が辞書順でソートされた suffix の開始位置を保持しているため、二分探索を用いて、高速にパターンマッチングできます。

banana の Suffix Array が求められているとして、Go で探索する実装例を示します。実装上の Suffix Array は 0-indexed とします。

  • Suffix Array を二分探索して、一致するすべての suffix を検索する実装例
main.go
package main

import (
	"fmt"
	"sort"
	"strings"
)

func main() {
	t := "banana"
	p := "an" // マッチングしたい文字列

	// banana の Suffix Array (0-indexed)
	sa := []int{5, 3, 1, 0, 4, 2}

	// strings.Compare の戻り値が 0 よりも大きいうちの最小の index を探索
	left := sort.Search(len(sa), func(i int) bool {
		return strings.Compare(t[sa[i]:min(sa[i]+len(p), len(t))], p) >= 0
	})

	// strings.Compare の戻り値が 1 である最小の index を探索
	right := sort.Search(len(sa), func(i int) bool {
		return strings.Compare(t[sa[i]:min(sa[i]+len(p), len(t))], p) == 1
	})

	for i := left; i < right; i++ {
		fmt.Printf("suffix: %s, match: %s\n", t[sa[i]:], t[sa[i]:sa[i]+len(p)])
	}
}

func min(a, b int) int {
	if a < b {
		return a
	} else {
		return b
	}
}
  • 出力結果
suffix: ana, match: an
suffix: anana, match: an

https://play.golang.org/p/JFNugaoB26N

このパターンマッチングは元の文字列 T の長さを として、マッチングしたい文字列 P の長さを とすると 時間でマッチングできます。Go の sort.Search 関数はソートされた配列やスライスに対して条件を満たす最小の index を二分探索できます。上記の実装では、suffix における prefix の先頭 len(p) 文字目までの部分文字列とマッチングしたい文字列 p を strings.Compare で比較し、結果が 0 以上と 1 となる最小の index 3を探索しています。Suffix Array に対して二分探索を行うことによって、パターンマッチングするときは、元の文字列の長さに対して、対数時間でおさえることができます。

Suffix Array の構築

Suffix Array を構築することを考えてみます。ナイーブに考えると、長さ の文字列 つをソートすることになります。クイックソートの 1 回あたりの平均計算量 とあわせて 時間になります。いかにして効率よく Suffix Array を構築できるかどうかがアルゴリズムのポイントになります。

  • ナイーブにソートして構築する実装例
main.go
package main

import (
	"fmt"
	"sort"
	"strings"
)

func main() {
	text := "banana"

	d := make([]data, 0, len(text))
	for i := 0; i < len(text); i++ {
		d = append(d, data{
			Index:  i,
			Suffix: text[i:],
		})
	}

	sort.Slice(d, func(i, j int) bool {
		ret := strings.Compare(d[i].Suffix, d[j].Suffix)
		if ret <= 0 {
			return true
		}
		return false
	})

	for _, v := range d {
		fmt.Printf("index: %d, suffix: %s\n", v.Index, v.Suffix)
	}
}

type data struct {
	Index  int
	Suffix string
}
  • 出力結果
index: 5, suffix: a
index: 3, suffix: ana
index: 1, suffix: anana
index: 0, suffix: banana
index: 4, suffix: na
index: 2, suffix: nana

https://play.golang.org/p/J97GtkfWBZp

しかし、構築に 時間かかるのでは、例えば 10 万文字程度の文字列の Suffix Array を構築するのにとても時間がかかるため、実用的ではありません。

  • ManberとMyersのアルゴリズム

そこで次は Manber と Myers によって示されたアルゴリズムを用いて構築することを考えてみます。基本的な着想はダブリングによるものです。つまり n 文字をソートするときに、まず 1 文字の部分文字列のみをソート、続いて 1 文字の部分文字列でソートした結果を用いて 2 文字の部分文字列をソート、、、と 2k 文字の部分文字列をソートするのに、k 文字の部分文字列でソートした結果を用います。詳しくは蟻本 1 を参照ください。蟻本が手もとにない場合は Suffix Array | Set 2 (nLogn Algorithm) などのページでアルゴリズムを確認ください。本記事では Go による実装のみを示します。ダブリングにより比較回数は 回で 1 回あたりのソートの平均計算量が ですから、全体では 時間のアルゴリズムです。

  • 蟻本ベースの Go による Suffix Array を構築する実装
suffixarray.go
package suffixarray

import (
	"sort"
)

type suffixArray struct {
	// length of input string
	N int

	// input text (ASCII only)
	Text string

	// Suffix Array
	Index []int
}

func New(text string) *suffixArray {
	var k int
	n := len(text)
	rank := make([]int, n+1)
	sa := make([]int, n+1)
	tmp := make([]int, n+1)

	for i := 0; i <= n; i++ {
		sa[i] = i
		if i < n {
			rank[i] = int(text[i])
		} else {
			rank[i] = -1
		}
	}

	cmp := func(i, j int) bool {
		if rank[sa[i]] != rank[sa[j]] {
			return rank[sa[i]] < rank[sa[j]]
		} else {
			ri, rj := -1, -1
			if sa[i]+k <= n {
				ri = rank[sa[i]+k]
			}
			if sa[j]+k <= n {
				rj = rank[sa[j]+k]
			}
			return ri < rj
		}
	}

	// k 文字についてソートされているところから、2k 文字をソートする
	for k = 1; k <= n; k *= 2 {
		sort.Slice(sa, cmp)
		tmp[sa[0]] = 0
		for i := 1; i <= n; i++ {
			tmp[sa[i]] = tmp[sa[i-1]]
			if cmp(i-1, i) {
				tmp[sa[i]]++
			}
		}
		for i := 0; i <= n; i++ {
			rank[i] = tmp[i]
		}
	}

	return &suffixArray{
		N:     n,
		Text:  text,
		Index: sa,
	}
}

banana の文字列で試しにテストしてみましょう。

suffixarray_test.go
package suffixarray

import (
	"testing"

	"github.com/google/go-cmp/cmp"
)

func TestNew(t *testing.T) {
	tests := []struct {
		name string
		text string
		want *suffixArray
	}{
		{
			name: "normal",
			text: "banana",
			want: &suffixArray{
				N:     6,
				Text:  "banana",
				Index: []int{6 /* contain empty string */, 5, 3, 1, 0, 4, 2},
			},
		},
	}
	for _, tt := range tests {
		t.Run(tt.name, func(t *testing.T) {
			got := New(tt.text)
			if diff := cmp.Diff(got, tt.want); diff != "" {
				t.Errorf("New() differs: (-got +want)\n%s", diff)
			}
		})
	}
}
  • テスト結果

テストが Pass することを確認できました。

=== RUN   TestNew
=== RUN   TestNew/normal
--- PASS: TestNew (0.00s)
    --- PASS: TestNew/normal (0.00s)
PASS

また Go で実装したライブラリは、国内のオンラインジャッジシステムの 1 つである Aizu Online Judge の Multiple String Matching という問題を用いて検証しました。05_maximum_00.in (1 MB程度あるので注意)のテストケースでタイムリミット超過(TLE)していましたが…

suffixarray パッケージによる Suffix Array の構築

さて、メインである本家の suffixarray パッケージを見てみましょう。Suffix Array の構築は New 関数を用いることができます。

New 関数で Suffix Array を構築し、Lookup メソッドや FindAllIndex メソッドなどを用いて Suffix Array から文字列のマッチングができます。banana の例であれば、以下のように結果を得ることができます。

main_test.go
package main

import (
	"fmt"
	"index/suffixarray"
)

func Example() {
	t := "banana"
	p := "an" // マッチングしたい文字列

	// Suffix Array の構築
	sa := suffixarray.New([]byte(t))

	// -1 でマッチングするすべての位置を取得。取得する index の順番はランダム
	indexes := sa.Lookup([]byte(p), -1)

	for _, i := range indexes {
		fmt.Printf("suffix: %s, match: %s\n", t[i:], t[i:i+len(p)])
	}
	// Unordered Output:
	// suffix: ana, match: an
	// suffix: anana, match: an
}

ベンチマーク

suffixarray パッケージの使い方が分かったところで蟻本ベースの Manber と Myers のアルゴリズムを用いて Suffix Array を構築する実装と、標準ライブラリを用いて構築する 2 つの方法でベンチマークを取得してみましょう。(なおベンチマークの結果はローカルの環境に依存します)

Suffix Array を構築する対象のデータは Multiple String Matching における 05_maximum_00.in のデータを用いました。100万文字あります。input データを読み込む時間はベンチマークからは除きます。

  • ベンチマークテスト
suffixarray_test.go
func BenchmarkLookupAll_my(b *testing.B) {
	data, err := ioutil.ReadFile("testdata/05_maximum_01.in.data")
	if err != nil {
		b.Fatalf("read test data: %v", err)
	}
	b.ResetTimer()

	New(string(data))
}

func BenchmarkLookupAll_std(b *testing.B) {
	data, err := ioutil.ReadFile("testdata/05_maximum_01.in.data")
	if err != nil {
		b.Fatalf("read test data: %v", err)
	}
	b.ResetTimer()

	suffixarray.New(data)
}
  • ベンチマーク結果
go test -bench . -benchtime=1000000000x
goos: windows
goarch: amd64
pkg: github.com/d-tsuji/go-sandbox
BenchmarkLookupAll_my-8         1000000000               4.54 ns/op
BenchmarkLookupAll_std-8        1000000000               0.0510 ns/op
PASS
ok      github.com/d-tsuji/go-sandbox      9.362s

ローカル環境でのベンチマークテストの結果によると、標準ライブラリは、私が実装した Manber と Myers のアルゴリズムに比べて、約 100 倍程度高速であることが分かります。

実は標準ライブラリの Suffix Array の構築アルゴリズムは SAIS 2 という Ge Nong、Sen Zhang、Wai Hong Chen によって提案された高速なアルゴリズムを用いています。SAIS の計算量は です。さらにいくつかのチューニングを施しており、詳しくは index/suffixarray/sais.go のドキュメントを確認ください。

ベンチマークでは約 100 倍程度の処理時間の違いがありましたが、上記の Manber と Myers のアルゴリズムの計算量が で SAIS の計算量が ですから、100 倍程度の差は自然です。SAIS を実装している Go の標準ライブラリが優秀であることが分かります。

まとめ

Go の標準ライブラリで私が面白いと思った suffixarray パッケージを紹介しました。suffixarray パッケージの構築アルゴリズムの計算量は で非常に高速です。その他に Manber と Myers による計算量 の構築アルゴリズムを用いた Go による実装を紹介しました。

参考

  • 岡野原大輔 (2012) 『高速文字列解析の世界』岩波書店
  1. 1.秋葉拓哉、岩田陽一、北川宜稔 (2012) 『プログラミングコンテストチャレンジブック [第2版]』 マイナビ出版 ↩
  2. 2.Two Efficient Algorithms for Linear Time Suffix Array Construction ↩
  3. 3.文字 a と b を strings.Compare(a, b) で辞書順で比較したときに a < b であれば -1、a = b であれば 0、a > b であれば +1 で返り値として取得できます。返り値が 0 以上の index を探索しているため a ≧ b である最小の index が取得できます。 ↩